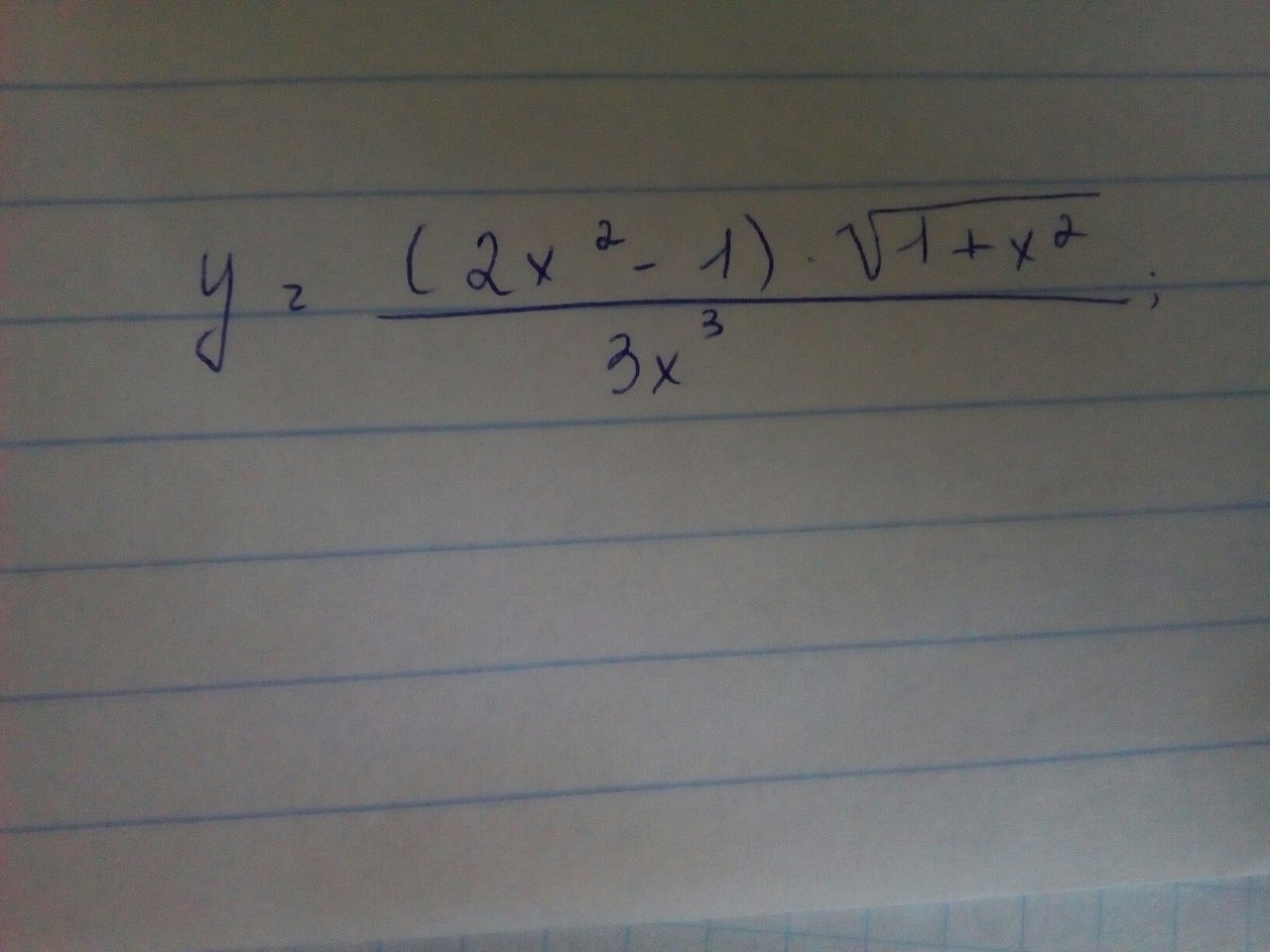Ответы
Ответ дал:
0
Найти производную 
Решение






Решение
Ответ дал:
0
спасибо большущее))
Ответ дал:
0
не могли бы еще с этим помочь ?https://znanija.com/task/21611112
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад