Question

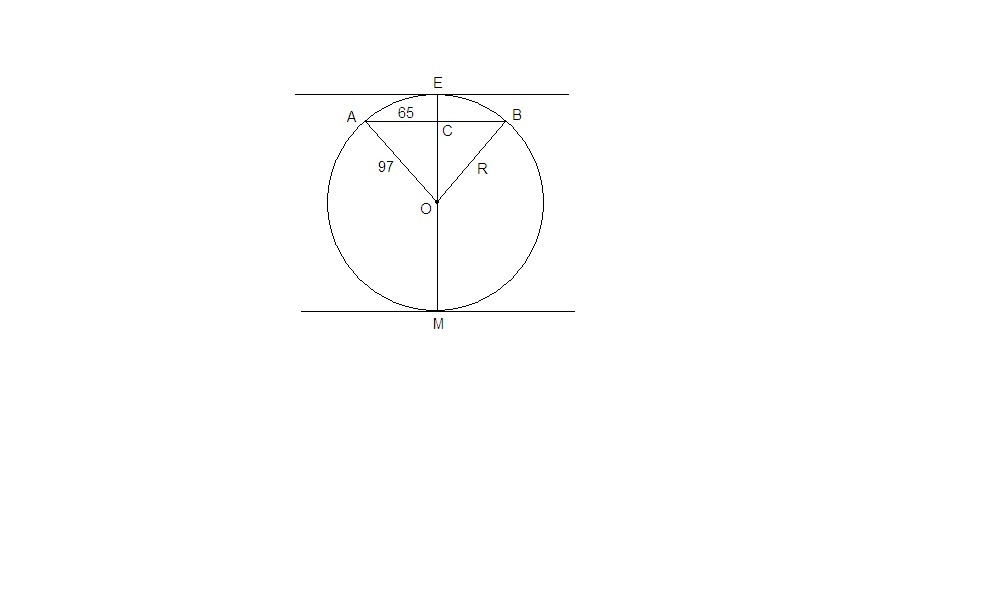
Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 97, длина хорды AB равна 130 .Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k

Answer 1

Пусть С - середина АВ. Тогда ОС - медиана и высота равнобедренного треугольника АОВ (ОА = ОВ = 97  как радиусы).
ΔАОС: по теореме Пифагора
           ОС =  √(ОА² - АС²) = √(97² - 65²) = √((97 - 65)(97 + 65)) = √(32 · 162) =
                 = √(2 · 16 · 2 · 81) = 2 · 4 · 9 = 72.
Так как касательная параллельна хорде АВ, то она перпендикулярна диаметру, на котором лежит ОС, таких касательных может быть две.
Тогда расстояние до касательной:
ЕС = R - OC = 97 - 72 = 25
или
СМ = R + OC = 97 + 72 = 169