Ответы
Ответ дал:
0
1 - метод Гаусса. получаем множество решений x1 = 1, x2-x3 = 3.
2 и 3 - метод Крамера и обратной матрицы: определитель равен нулю, значит, система не не может быть решена этим методом.
Приложения:
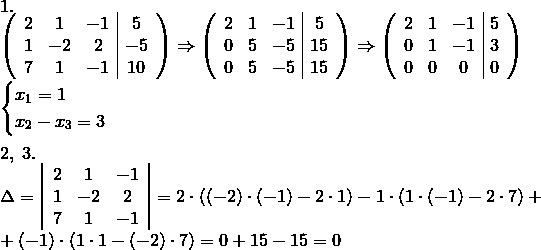
Вас заинтересует
7 лет назад
10 лет назад
10 лет назад
