Ответы
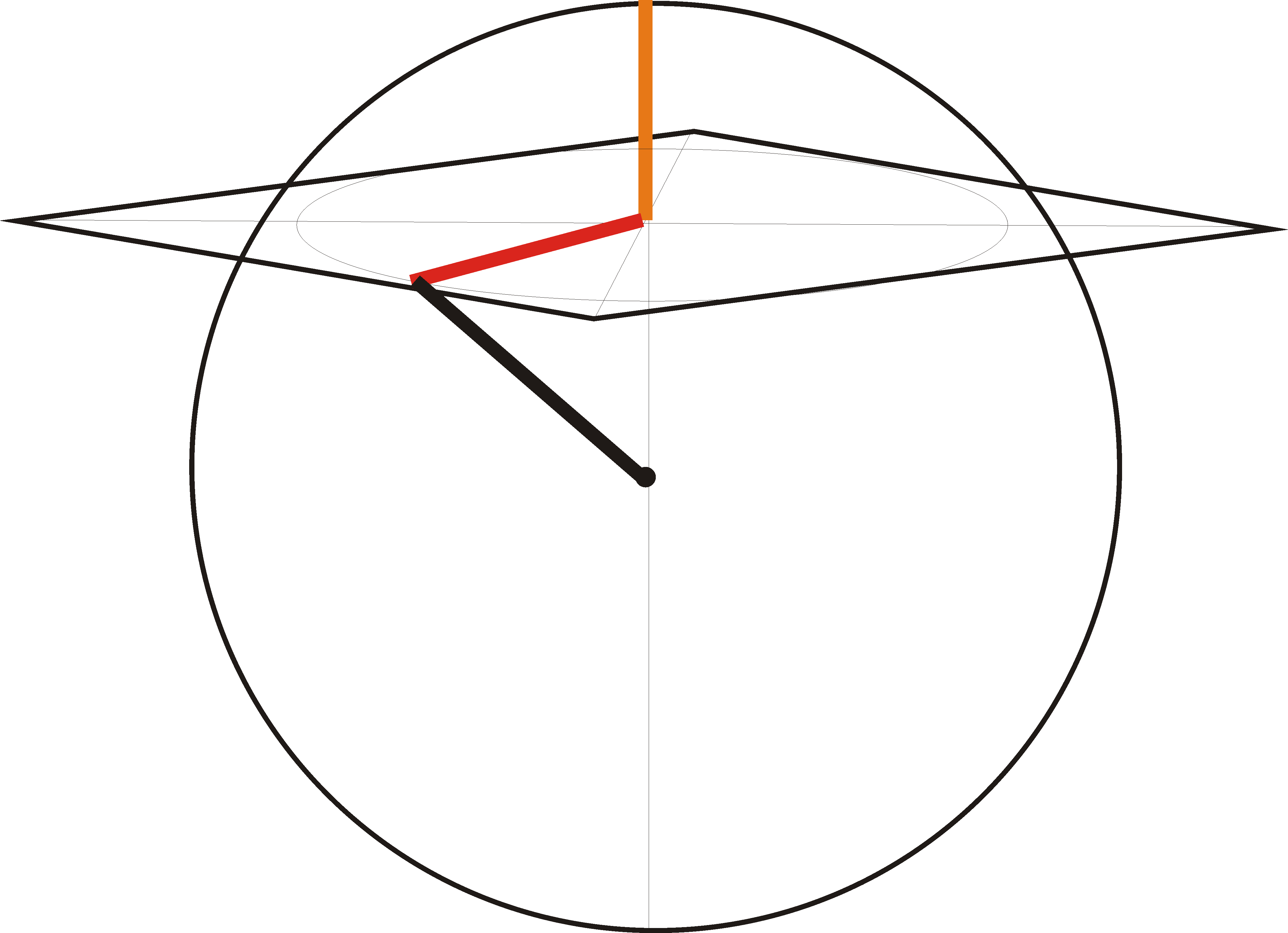
Плоскость ромба отсекает от шара сегмент высотой 5 - 3 = 2. Квадрат радиуса основания этого сегмента (радиуса вписанной в ромб окружности) равен 2(2*5 - 2) = 2*8 = 16. Тогда радиус равен 4.
Итак, у нас есть ромб со стороной 7 (по условию) и радиусом вписанной в него окружности, равным 4. Находим площадь. Она равна половине произведения его диагоналей.
Радиус вписанной в ромб окружности есть высота, выведенная из прямого угла его четверти (т.е. одного из четырех прямоугольных треугольников, на которые диагонали разбивают ромб).
Произведение половин диагоналей ромба - произведение катетов такого треугольника - равно 4(высота)*7(гипотенуза - сторона ромба) = 28. Тогда половина произведения диагоналей ромба (т.е. его площадь) будет равна 28*2 = 56.
Ответ: 56.
Прошу прощения за рисунок - наскоро.
Остались вопросы - пожалуйста, в личку!