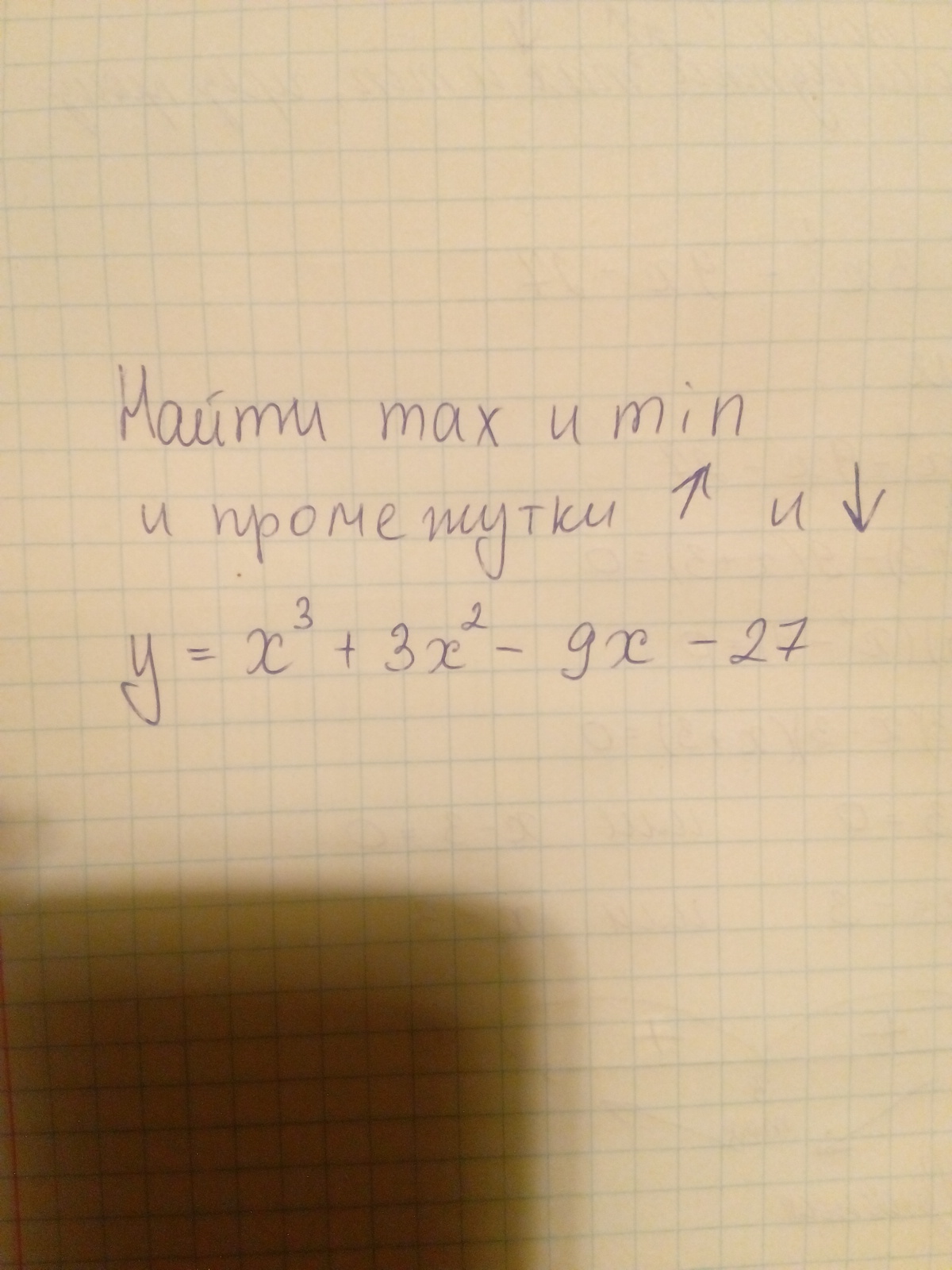Ответы
Ответ дал:
0
Надо методом производных - вычисляем производную.
РЕШЕНИЕ
Y = x³ + 3x² - 9x - 27 - функция.
Первая производная.
Y' = 3x² - 6x - 9.
Точки экстремума - нули производной - решаем квадратное уравнение.
Дискриминант - D=144 и √144 = 12 и х1 = -1 и х2 = 3.
Подставили значения в функцию.
Y(1) = -32 - минимум
Y(-3) = 0 - максимум.
Возрастает - Х∈(-∞,-3]∪[0, +∞)
Убывает - Х∈[-3,0]
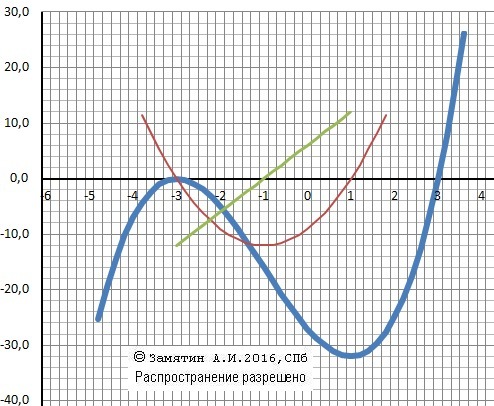
График для наглядности.
Точка перегиба - вторая производная - зеленая прямая.
РЕШЕНИЕ
Y = x³ + 3x² - 9x - 27 - функция.
Первая производная.
Y' = 3x² - 6x - 9.
Точки экстремума - нули производной - решаем квадратное уравнение.
Дискриминант - D=144 и √144 = 12 и х1 = -1 и х2 = 3.
Подставили значения в функцию.
Y(1) = -32 - минимум
Y(-3) = 0 - максимум.
Возрастает - Х∈(-∞,-3]∪[0, +∞)
Убывает - Х∈[-3,0]
График для наглядности.
Точка перегиба - вторая производная - зеленая прямая.
Приложения:
Ответ дал:
0
Большое вам спасибо))
Ответ дал:
0
Подскажи пожалуйста, как проверяют промежутки возрастания и убывания?
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад