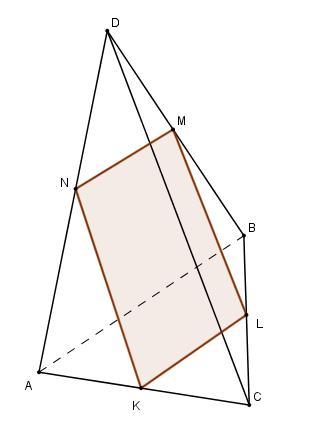
В тетраэдре АВСД точки К, L , M, N - середины ребер АС , ВС , ВД . АД соответственно . Определите вид четырехугольника KLMN и его периметр,если AB=16 см и СД =18 см .
Ответы
Ответ дал:
0
Поскольку KL, MN, NK, ML соединяют середины ребер, то они являются средними линиями треугольников ABC, ADB, ADC, DBC, соответственно. По свойству средней линии треугольника
MN || AB, см
KL || AB, см, значит KL || MN и KL=MN
NK || CD, см
ML || CD, см, следовательно, ML || NK и ML=NK
Так как у четырехугольника противоположные стороны равны, то MNKL - параллелограмм.
P(MNKL) = 2 * (NK + MN) = 2 * (9 + 8) = 34 см.
Ответ: 34 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад