Question

Помогите!!!! y=x3-3x2-1 .
Для данной функции y=f(x) найдите:
a) Область определения функции D(f).
b) Производную и критические точки.
c) Промежутки монотонности.
d) Точки экстремума и экстремумы функции.
e) Точки пересечения графика функции с осями координат и дополнительные точки.
f) Постройте график функции.

Answer 1

ДАНО
Y= x² - 3x - 1
ИССЛЕДОВАНИЕ
1. Область определения - непрерывность - разрывов нет.
Х∈(-∞,+∞) или Х∈R.
2. Пересечение с осью Х   ~ 3.2 (сложная формула)  - один корень.
3. Пересечение с осью У - У(0) = -1
4. Поведение на бесконечности
Y(-∞) = -∞ ,  Y(+∞) = +∞
5. Проверка на четность.
Y(x) = x³-3x²-1
Y(-x) = -x³-3x²-1
Y(-x) ≠ Y(x) - функция не четная ни нечетная.
6. Производная функции.
Y' = -3x²-6x =-3*x*(x+2).  Корни - х1 = 0,  х2 = 2.
7. Локальные экстремумы - в корнях производной.
Ymax(0) = -1 - максимум
Ymin(2) = -5 - минимум.
8. Монотонность функции.
Возрастает - X∈(-∞,0]∪[2,+∞)
Убывает - X∈[0,2].
9. Вторая производная.
Y" = -6x-6 = -6*(x+1).
10. Точка перегиба - Y"(x) = 0, х = 1, у = -3.
Выпуклая - "горка" - X∈(-∞,1]
Вогнутая - "ложка" - X∈[1,+∞).
11. Дополнительные точки.
Y(-2) = -22 и Y(-1) = 6 и Y(0) = -2 и Y(2) = -6 и Y(3) = -2 и Y(4) = 14.
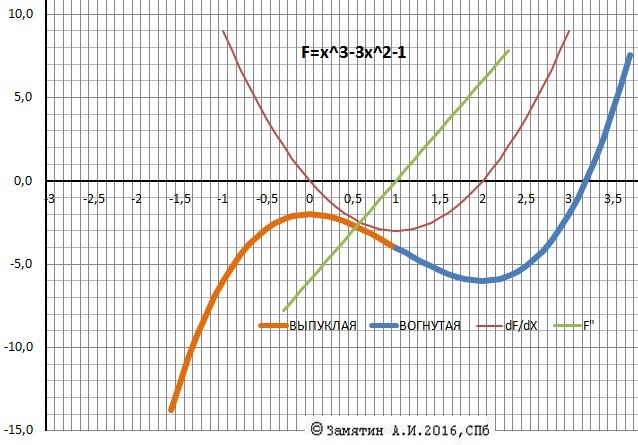
12. График прилагается.