Ответы
Ответ дал:
0
Ответ ответ ответ ответ ответ ответ ответ
Приложения:
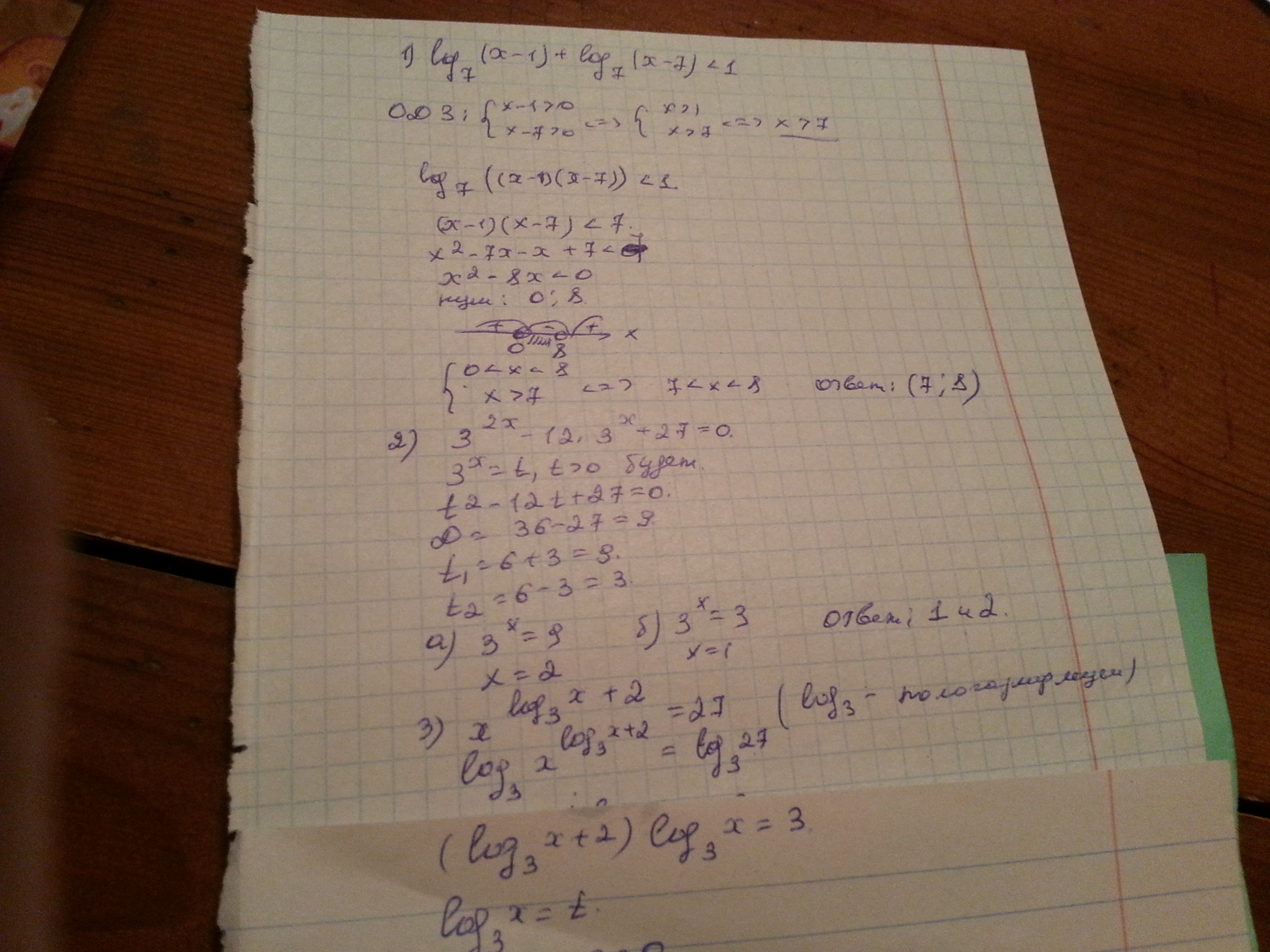
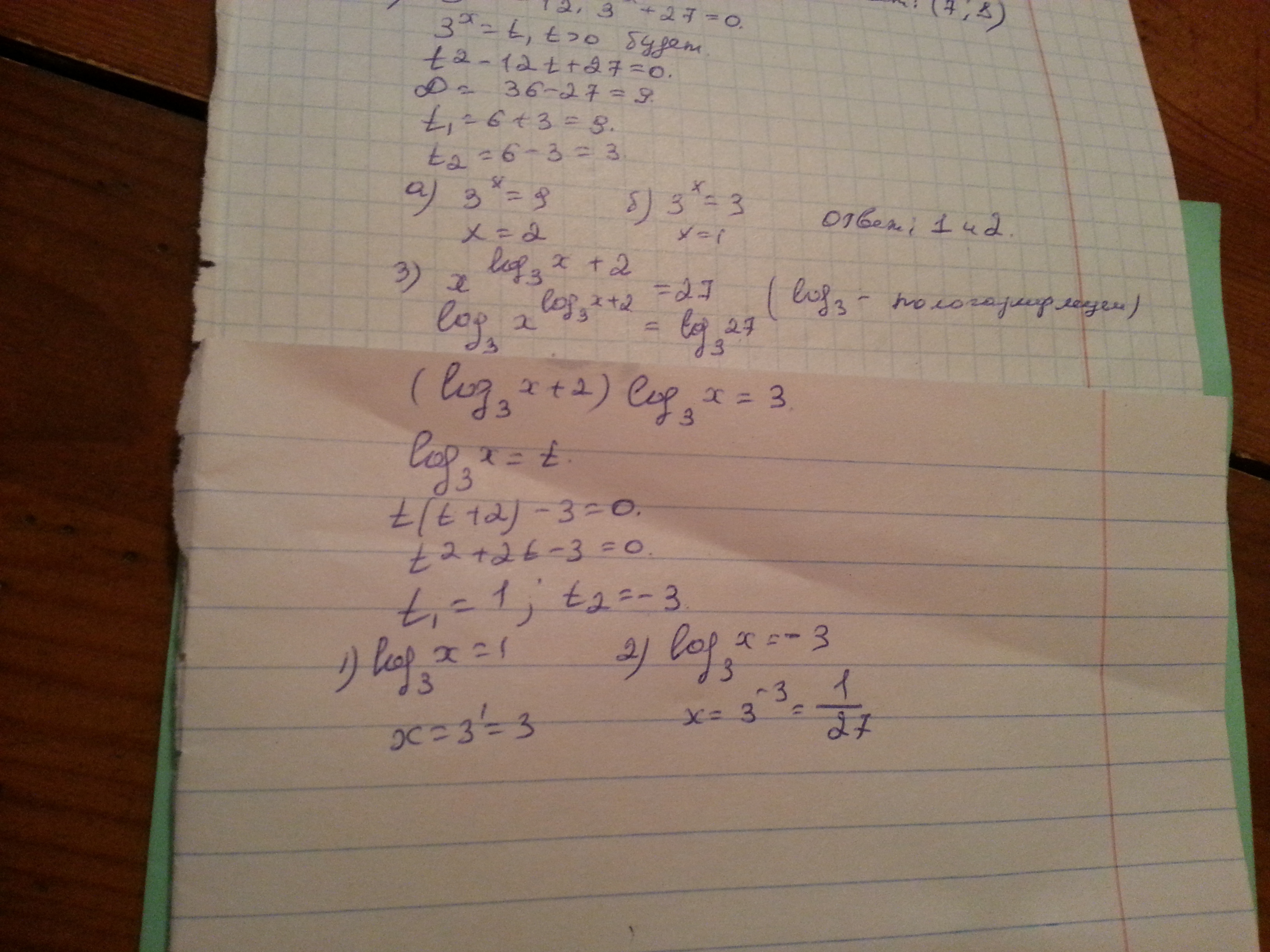
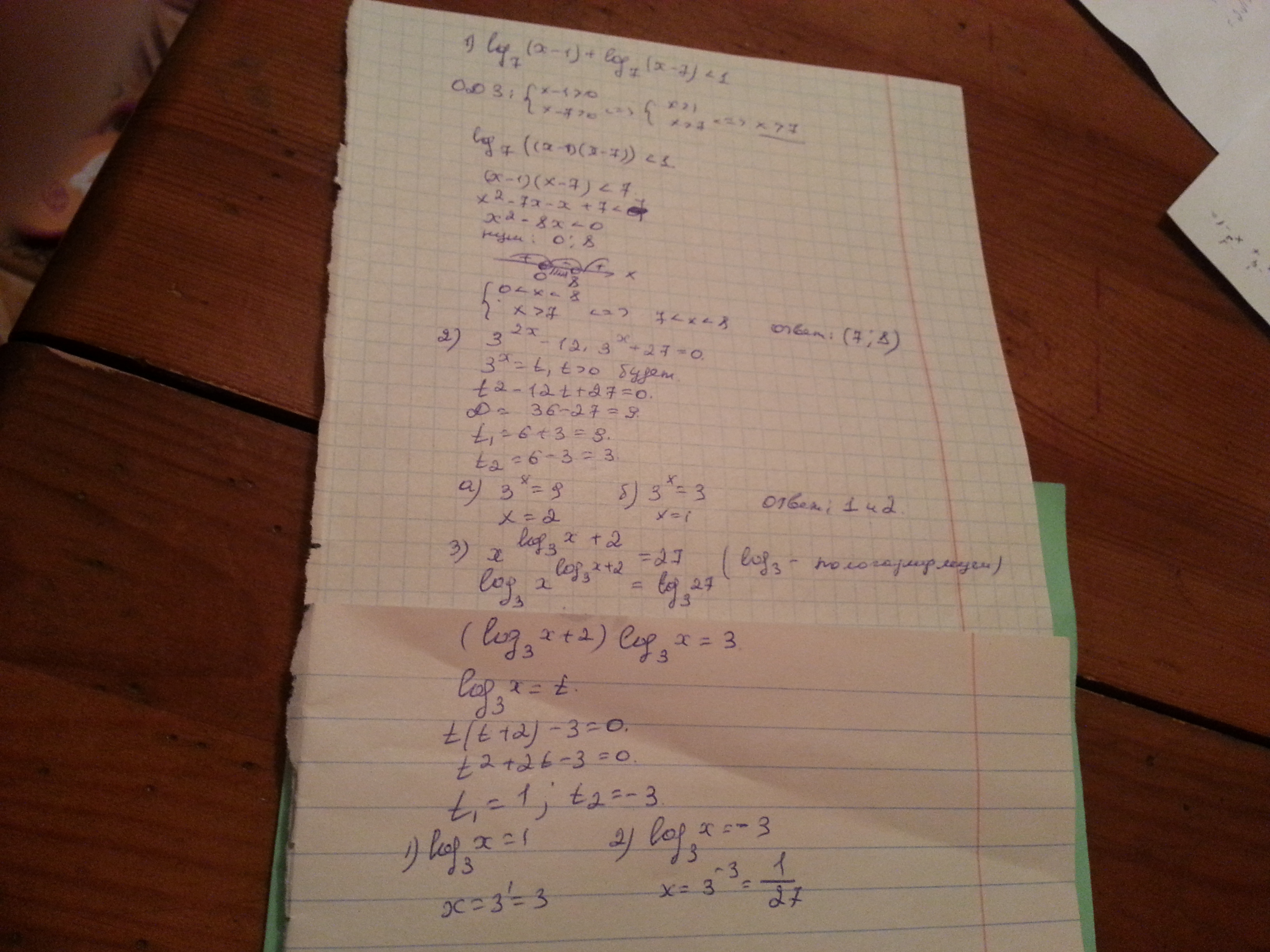
Ответ дал:
0
спасиииииииииииииииииииибо
Ответ дал:
0
log7(x-1)+log7(x-7)<1
Нужно найти все значения x-1 при которых аргумент логарифма положителен :
И найти все значения x-7 при которых аргумент логарифма положителен :
{x-1≤0
{x-7≤0
{x≤1
{x≤7
Пиши без шагов, просто я пишу подробней, чтобы ты/вы понял(ли)
1)Исключить все допустимые значения :
log7(x-1)+log7(x-7)<1; x>1; x>7
2)Определить пересечение заданных множеств значений:
log7(x-1)+log7(x-7)<1; x€(7;+бесконечность)
3)Далее упростить выражение по формуле:
loga(x)+loga(y)=loga(x•y)
log7((x-1)•(x-7))<1
4)Перемножить выражение в скобках:
log7(x•x-x•7-x-1•(-7))<1
5) Используй(те) переместительный закон, и закон умножения:
log7(x^2-7x-x+7)<1
6) Подобные
log7(x^2-8x+7)<1
7)После, loga(x)<b, при условии что a>1 равносильно x<a^b
x^2-8x+7<7^1
x^2-8x+7<7
7.1) Сократим
x^2-8x<0
7.2) выносим общий множитель за скобки
x(x-8)<0
8) Существует два случая когда a•b<0
1случай-{a<0 ; 2случай-{a>0 ;
{b>0 ; {b<0 ;
8) Решаем функцию:
{x<0
{x-8>0
{x>0
{x-8<0
{x<0
{x>8
{x>0
{x<8
9) x€∅
x€(0;8)
10)найдите объединение:
x€(0;8), x€(7;+бесконечность)
11) Окончательным решением является пересечение множества решений и области допустимых значений:
x€(7;8);
Нужно найти все значения x-1 при которых аргумент логарифма положителен :
И найти все значения x-7 при которых аргумент логарифма положителен :
{x-1≤0
{x-7≤0
{x≤1
{x≤7
Пиши без шагов, просто я пишу подробней, чтобы ты/вы понял(ли)
1)Исключить все допустимые значения :
log7(x-1)+log7(x-7)<1; x>1; x>7
2)Определить пересечение заданных множеств значений:
log7(x-1)+log7(x-7)<1; x€(7;+бесконечность)
3)Далее упростить выражение по формуле:
loga(x)+loga(y)=loga(x•y)
log7((x-1)•(x-7))<1
4)Перемножить выражение в скобках:
log7(x•x-x•7-x-1•(-7))<1
5) Используй(те) переместительный закон, и закон умножения:
log7(x^2-7x-x+7)<1
6) Подобные
log7(x^2-8x+7)<1
7)После, loga(x)<b, при условии что a>1 равносильно x<a^b
x^2-8x+7<7^1
x^2-8x+7<7
7.1) Сократим
x^2-8x<0
7.2) выносим общий множитель за скобки
x(x-8)<0
8) Существует два случая когда a•b<0
1случай-{a<0 ; 2случай-{a>0 ;
{b>0 ; {b<0 ;
8) Решаем функцию:
{x<0
{x-8>0
{x>0
{x-8<0
{x<0
{x>8
{x>0
{x<8
9) x€∅
x€(0;8)
10)найдите объединение:
x€(0;8), x€(7;+бесконечность)
11) Окончательным решением является пересечение множества решений и области допустимых значений:
x€(7;8);
Приложения:
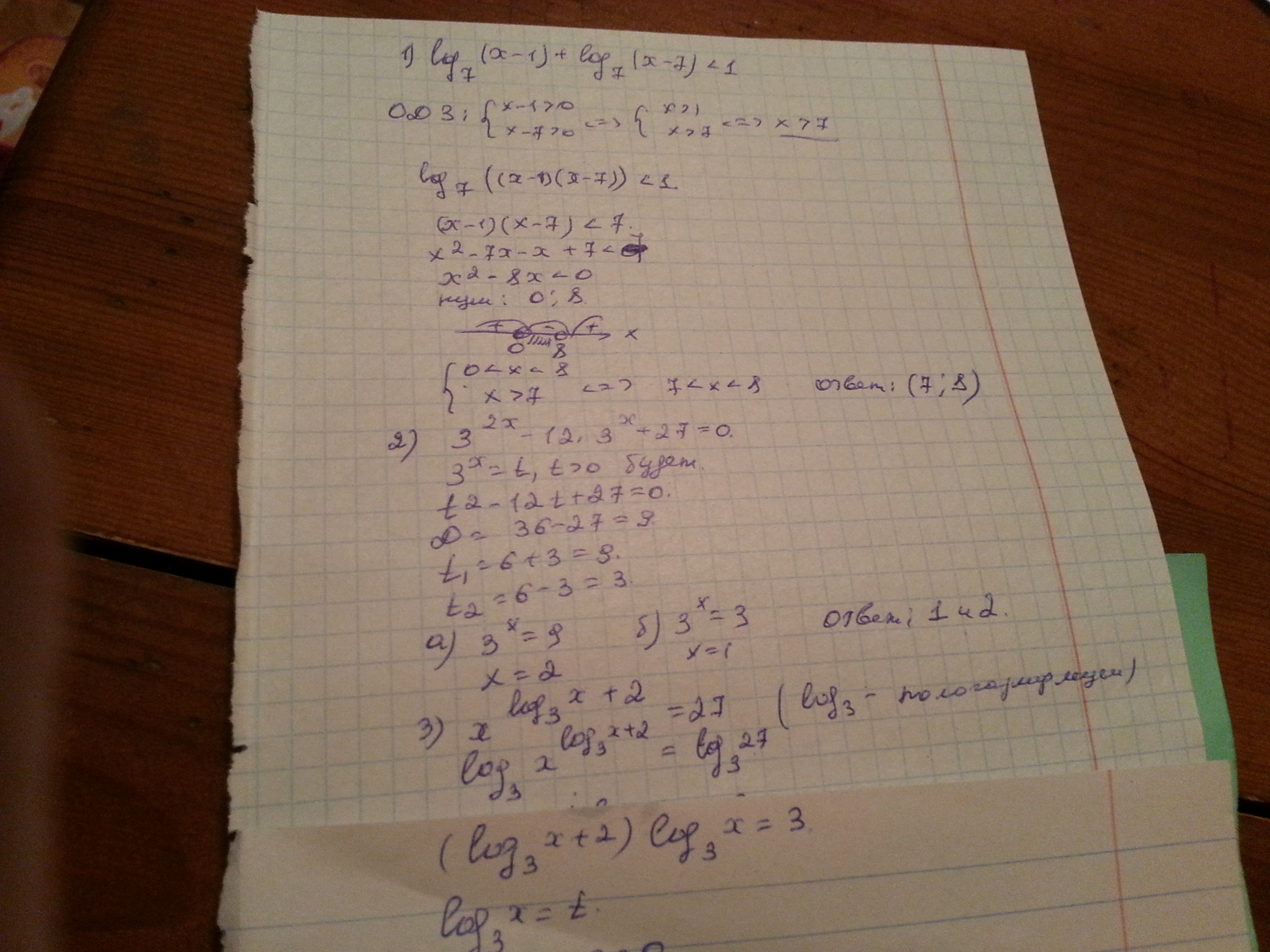
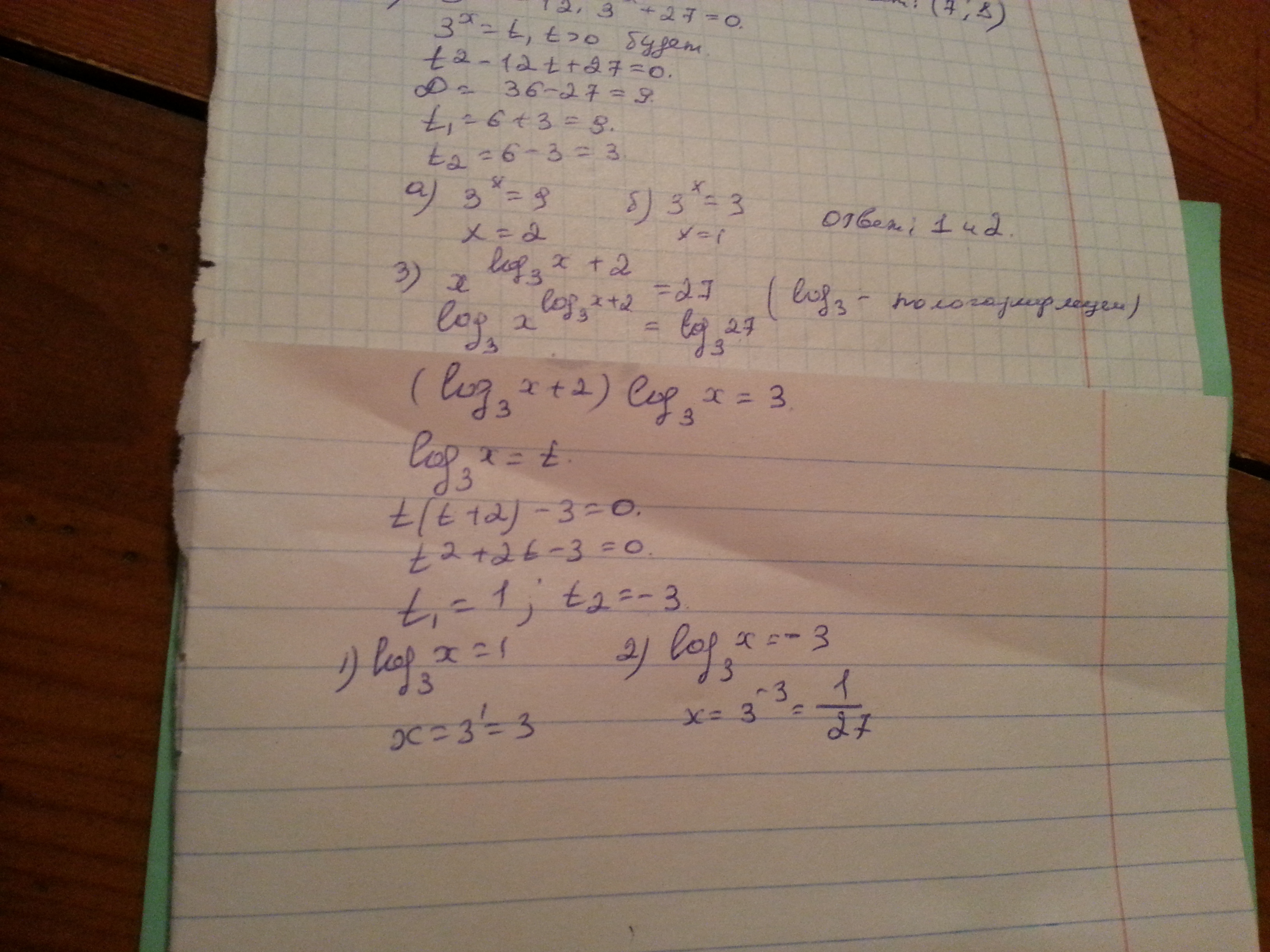
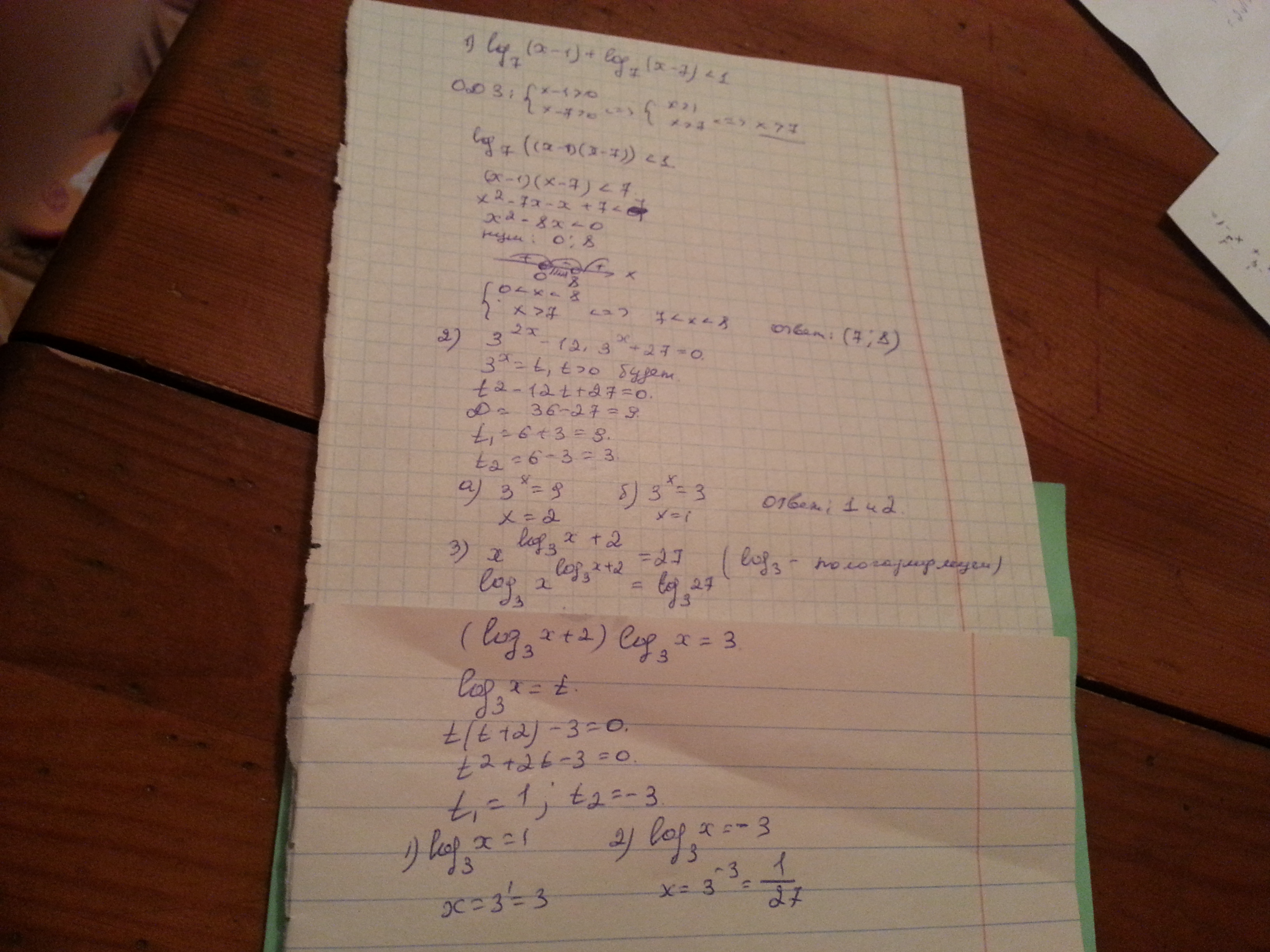
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
