Question

Докажите,что в прямоугольном треугольнике медиана и высота,проведенные к гипотенузе,образуют угол,равный разности острых углов треугольника.Спасибо!

Answer 1

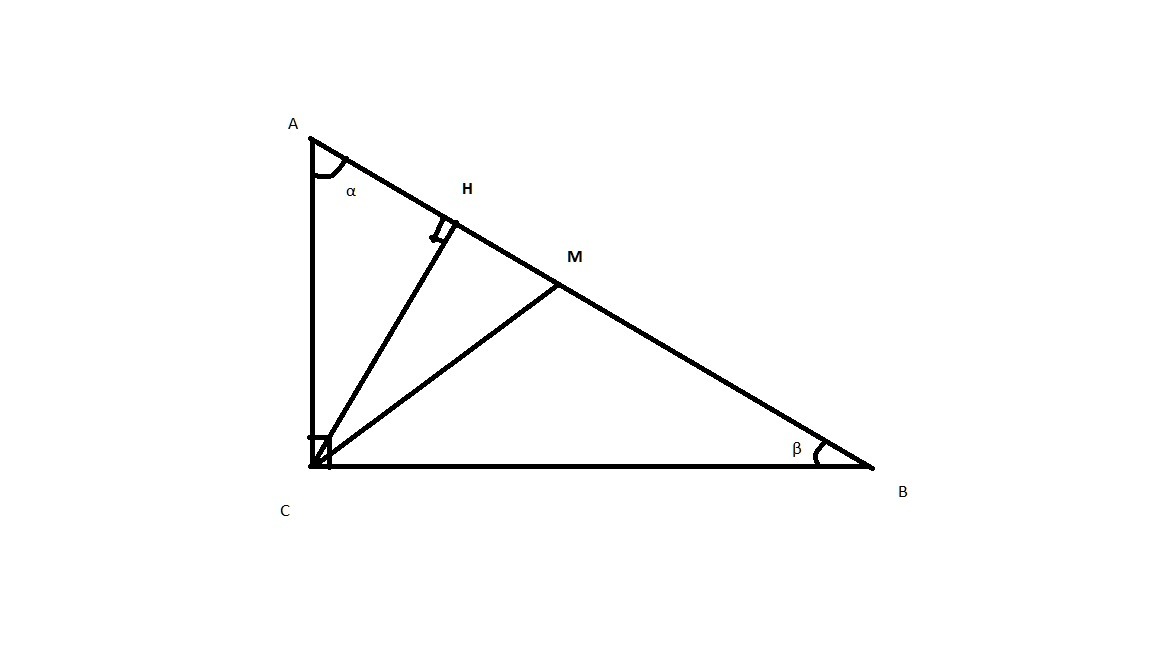
Пусть дан некоторый треугольник ABC с медианой CM и высотой CH и острыми углами β и α.

Из прямоугольного треугольника AHC найдем угол ACH=90-α
Из равнобедренного треугольника BHC (свойство медианы, проведенной из прямого угла) угол MCB=MBC=β

Угол MCH=ACB-MCB-ACH
MCH=90-(90-α)-β=90-90+α-β=α-β

Теорема доказана.

Answer 2

Огромное спасибо!Добра вам