Question

расмотрите рисунок , и докажите что [AM] является биссектрисой треугольника ABC

Answer 1

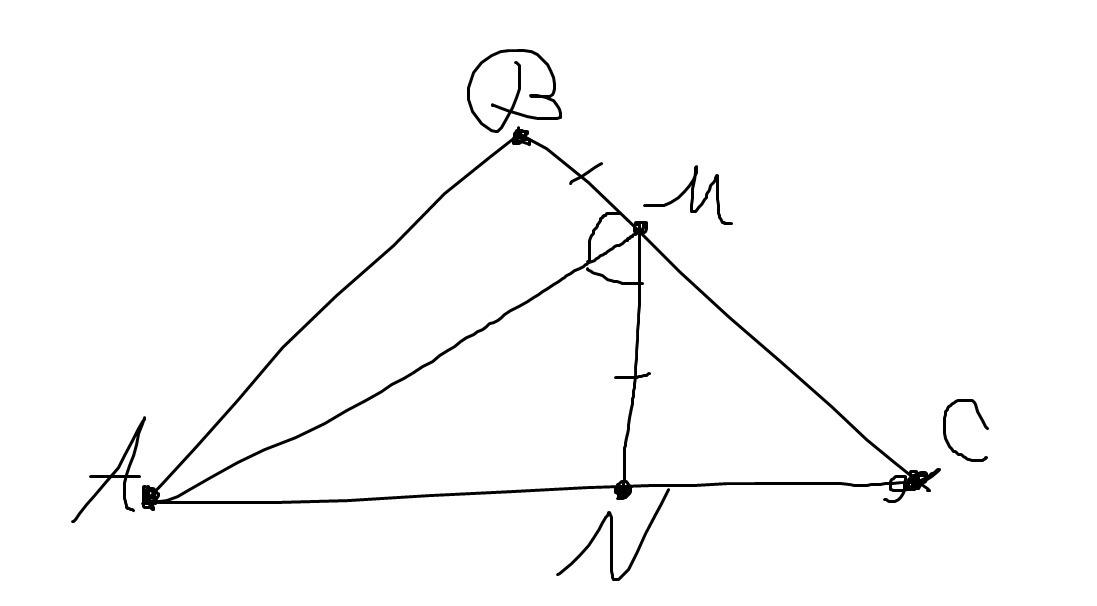
Рассмотрим ∆ABM и ∆ANM
BM = MN
угол BMA = углу NMA
AM - общая сторона

Значит, ∆ABM = ∆ANM - по I признаку равенства треугольников

Из равенства треугольников => угол BAM = углу MAN => AM - биссектриса, т.к. она делит угол на два рпаныхн между собой угла.

Answer 2

стоп

Answer 3

[AM] является биссектрисой треугольника ABC

Answer 4

ключевое

Answer 5

Тут доказано, что АМ является биссектрисой