Question

40 БАЛЛОВ, 1 задание, с рисунком.
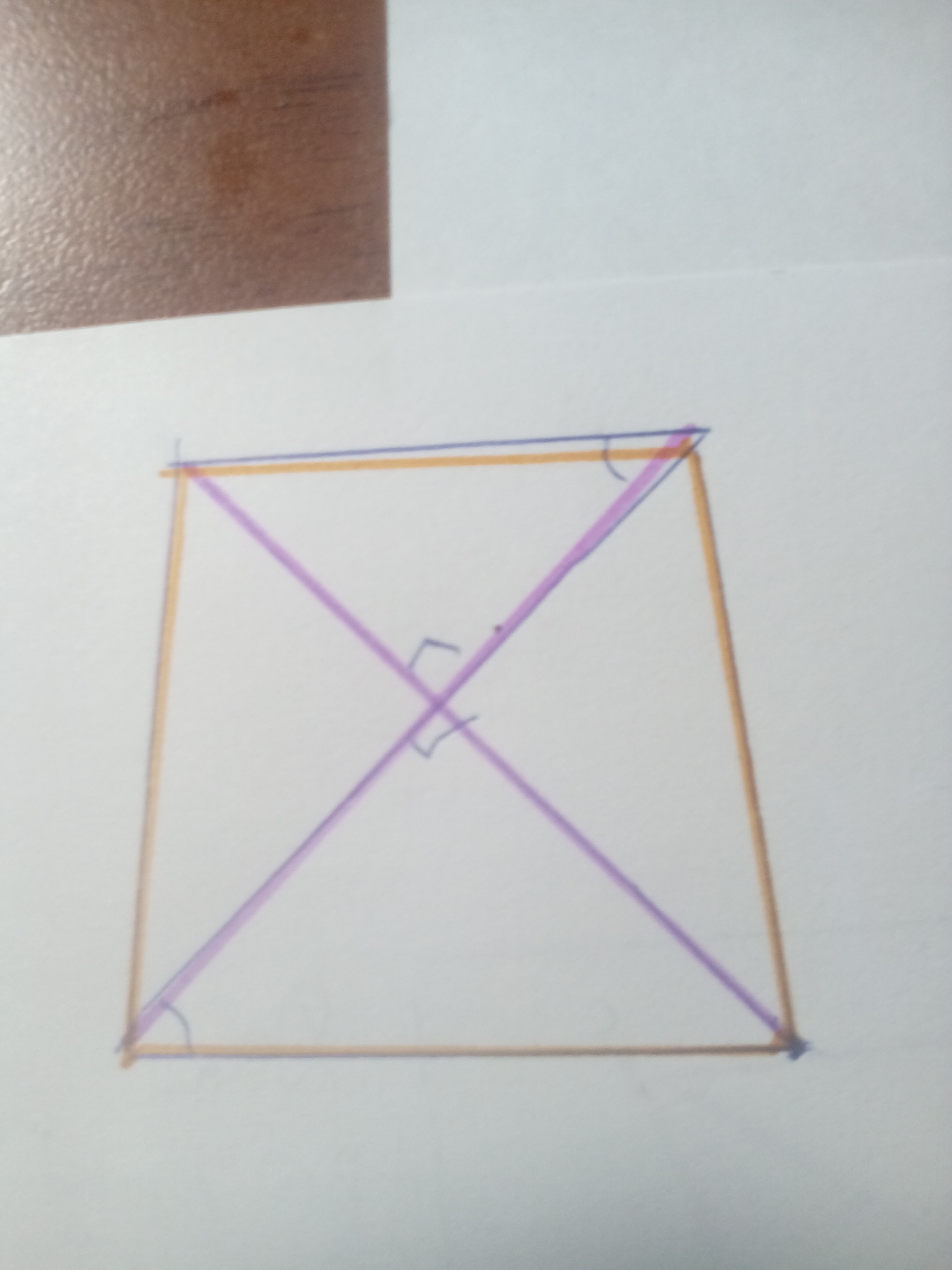
Найдите высоту трапеции, если ее диагонали взаимно перпендикулярны и равны
15 и 20.

Answer 1

Площадь любого четырёхугольника равна половине произведениях диагоналей на синус угла между ними.
Т.к. угол между диагоналями равен 90°, то синус угла между ними равен 1.
Тогда = 1/2•15•20•1 = 150.
В трапеции, у которой диагонали перпендикулярны друг другу, средняя линия равна высоте. Площадь трапеции равна произведению высоты на среднюю линию, тогда высота равна √S = √150 = 5√6.

Answer 2

Ой, я только площадь нашёл. Сейчас дорешаю и рисунок скину.

Answer 3

Такой простой рисунок?

Answer 4

Да. Но для полного решения лучше все-таки опустить высоту к большему основанию)

Answer 5

Ага, поняла, спасибо спасли.

Answer 6

Не за что)