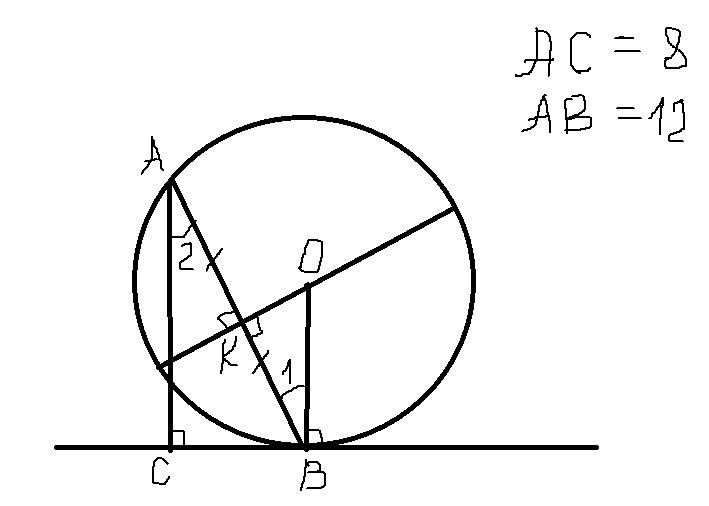Пожалуйста решите задачу по геометрии. Кто решит отблаагодарю. Длина хорды равна 12 см. Через один из концов этой хорды проведена касательная расстояние которой от другого конца равно 8 см. найти радиус круга. решите пожалуйста о рисунке уже не прошу ну хотябы решите только правельно, можно коротко и с рисунком а можно и без рисунка.
Ответы
Рисунок во вложении.
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
Ответ: 9см.