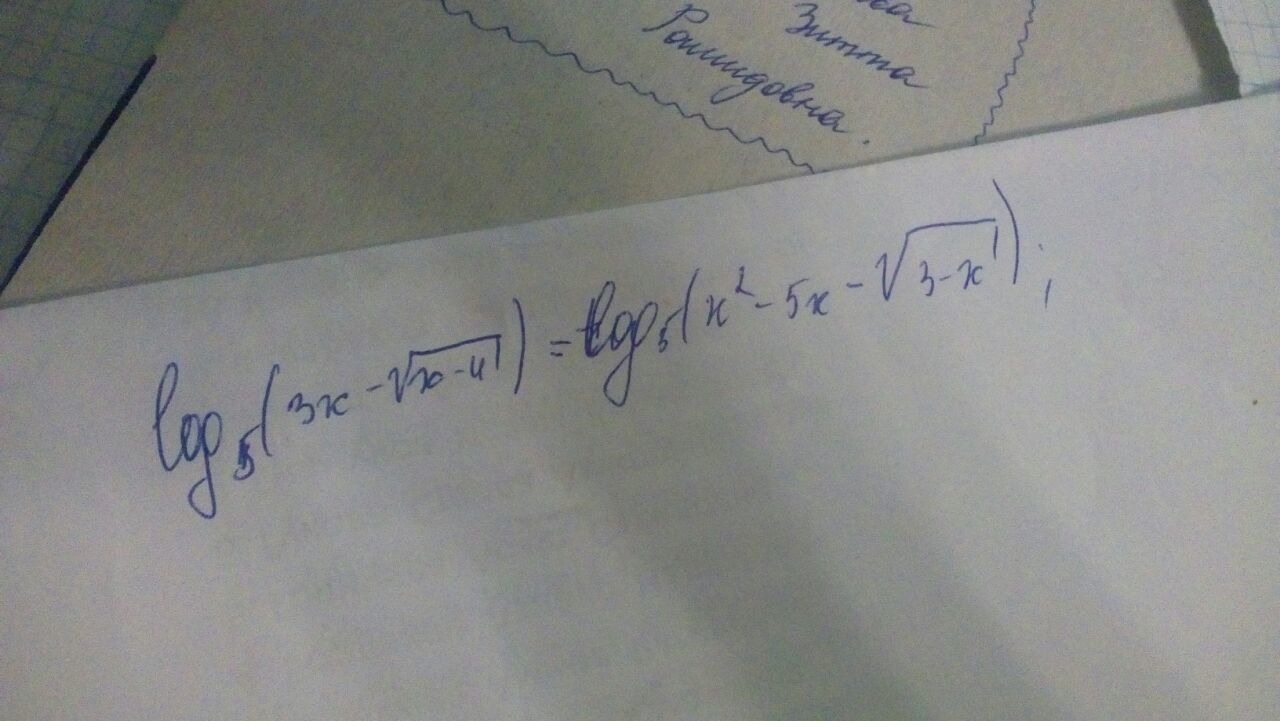Ответы
Ответ дал:
0
Для начала найдем ОДЗ:
Логарифмируемое выражение должно быть больше нуля

Корней нет, ветви параболы направлены вверх, значит x²-x+4 >0 при любых "х"
Итак, решение первого неравенства системы: х≥4

Дальше не имеет смыла решать систему:
в первом неравенстве x≥4, во втором, если система и имеет решение, то при х≤3.
В таком случае нет общих точек, удовлетворяющих обоим неравенствам системы:
 - нет решений.
- нет решений.
Если ОДЗ не имеет решений, значит и само уравнение не имеет корней
ОТВЕТ: корней нет
Логарифмируемое выражение должно быть больше нуля
Корней нет, ветви параболы направлены вверх, значит x²-x+4 >0 при любых "х"
Итак, решение первого неравенства системы: х≥4
Дальше не имеет смыла решать систему:
в первом неравенстве x≥4, во втором, если система и имеет решение, то при х≤3.
В таком случае нет общих точек, удовлетворяющих обоим неравенствам системы:
Если ОДЗ не имеет решений, значит и само уравнение не имеет корней
ОТВЕТ: корней нет
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад