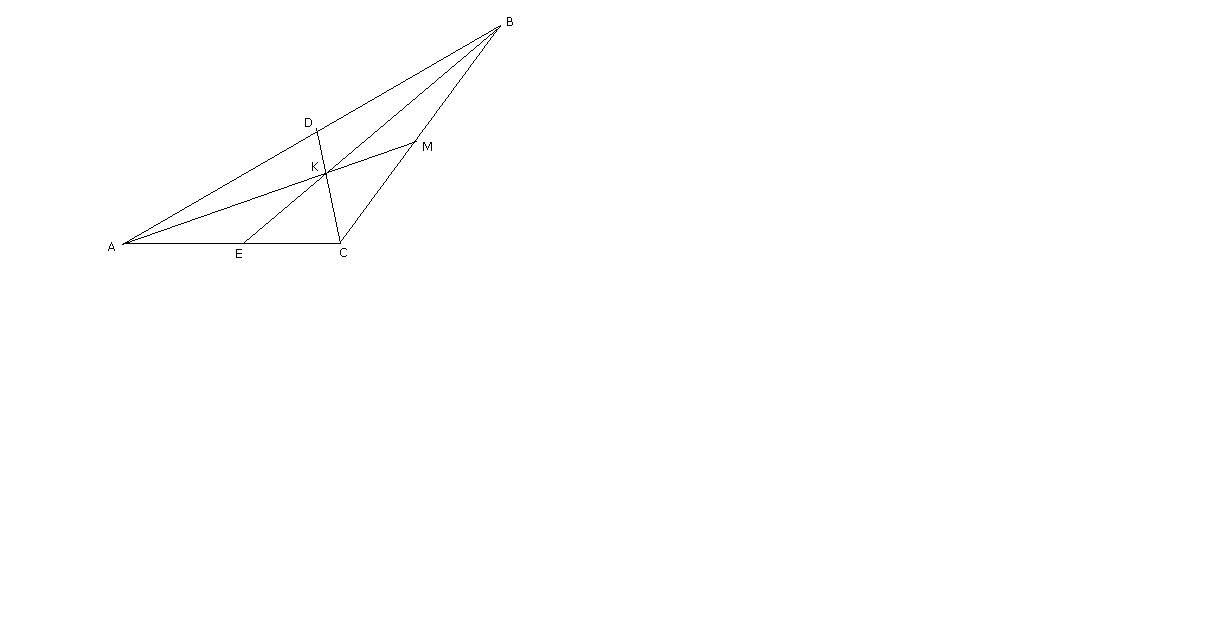
В треугольнике ABC медианы CD и BE пересекаются в точке K. Найдите площадь четырёхугольника ADKE, если BC = 20, AC = 12, угол ACB = 135 градусов.
Ответы
Ответ дал:
0
Медианы делят треугольник на 6 равновеликих (равных по площади).
Четырехугольник ADKE состоит из двух таких треугольничков.
Найдем площадь треугольника ВЕС:
S (BEC) = 1/2 BC*EC*sin 135° = 1/2 20*6*√2/2 =30√2 (под корнем только 2)
ΔBEC состоит из трех равновеликих треугольников, значит площадь одного 10√2.
S (ADKE)= 10√2*2 = 20√2
Четырехугольник ADKE состоит из двух таких треугольничков.
Найдем площадь треугольника ВЕС:
S (BEC) = 1/2 BC*EC*sin 135° = 1/2 20*6*√2/2 =30√2 (под корнем только 2)
ΔBEC состоит из трех равновеликих треугольников, значит площадь одного 10√2.
S (ADKE)= 10√2*2 = 20√2
Приложения:
Ответ дал:
0
sps
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад