Ответы
Ответ дал:
0
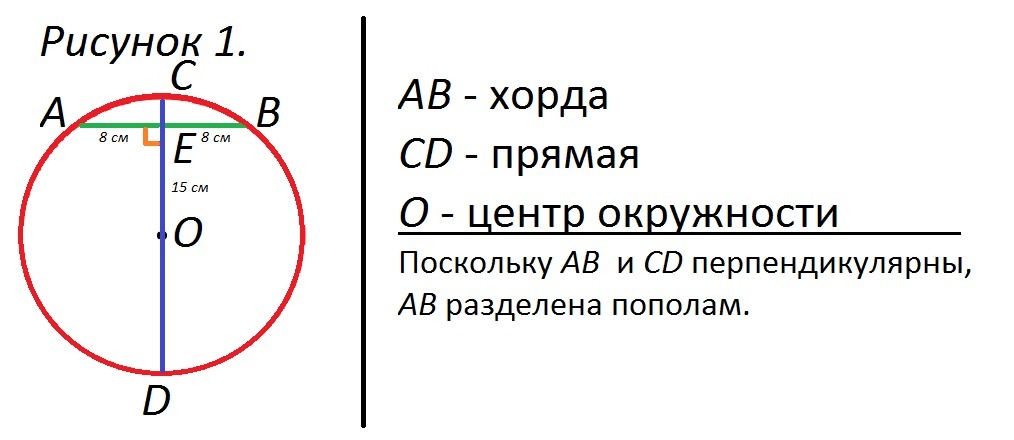
Проведём прямую, проходящую через центр окружности и перпендикулярной хорде (в этом случае прямая делит хорду пополам). Смотри Рисунок 1.
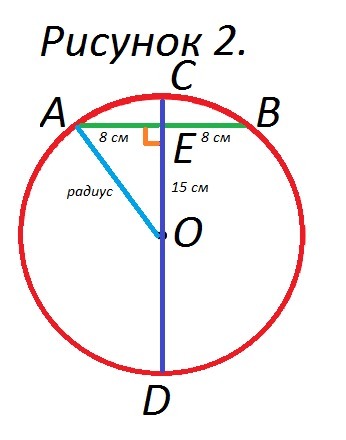
Начертим радиус . Тогда образуется прямоугольный треугольник,
. Тогда образуется прямоугольный треугольник,  и
и  становятся катетами, а радиус
становятся катетами, а радиус  - гипотенузой.
- гипотенузой.
Смотри Рисунок 2.
Радиус находится по Теореме Пифагора. Сумма квадратов катетов = квадрат гипотенузы.






Ответ: радиус равен 17 сантиметрам.
Начертим радиус
Смотри Рисунок 2.
Радиус находится по Теореме Пифагора. Сумма квадратов катетов = квадрат гипотенузы.
Ответ: радиус равен 17 сантиметрам.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад