Найти tg альфа/2, если sin альфа = 1/3 и П/2 больше или равен альфа, а альфа больше или равен П.
Задание №40.68.
Приложения:
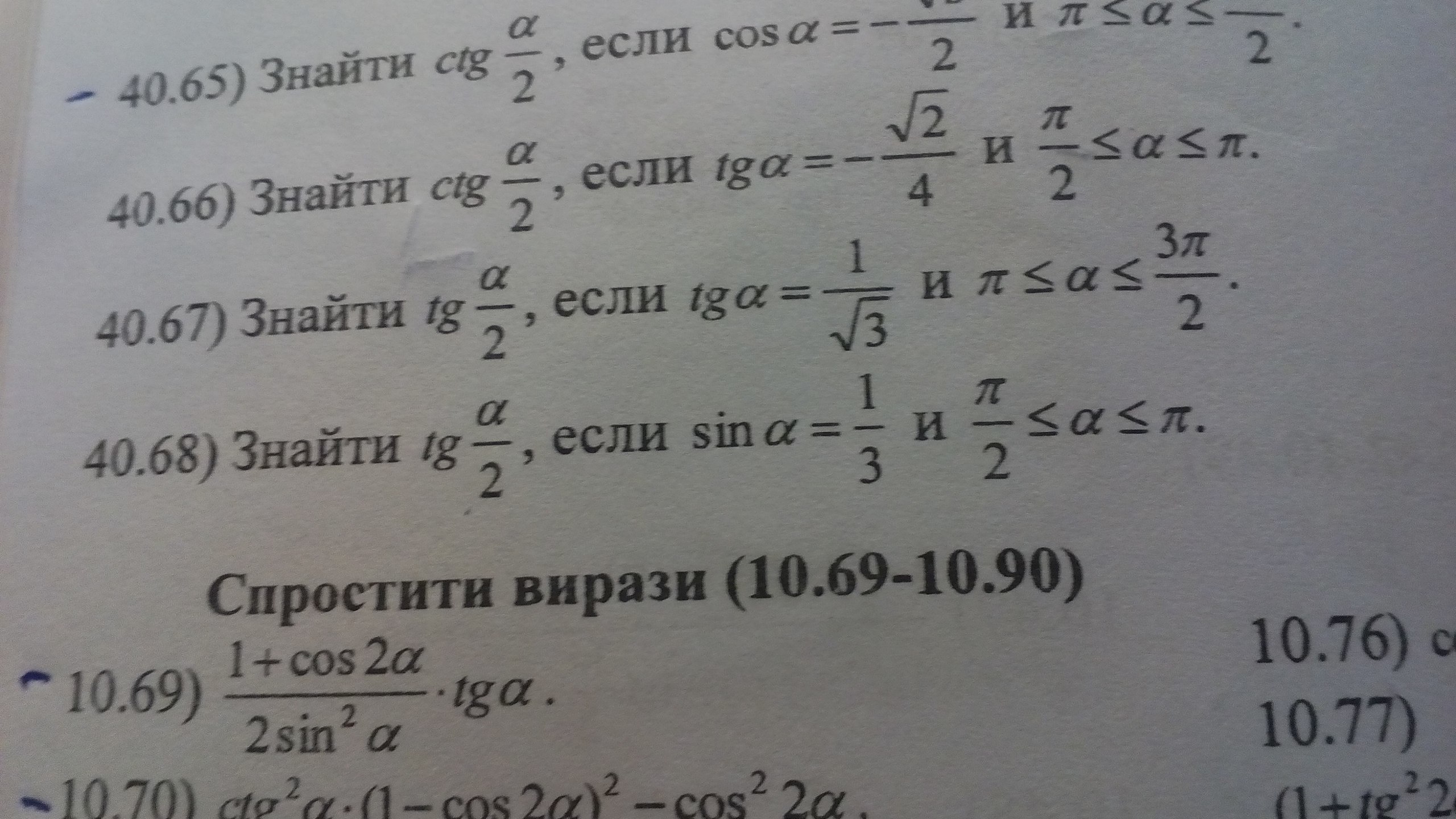
Ответы
Ответ дал:
0
cos²(α)=1-sin²(α)=1-1/9=8/9. А так как угол α лежит во 2 четверти, то cos(α)<0. Тогда cos(α)=-√8/9=-2*√2/3. tg(α/2)=(1-cos(α))/sin(α)=3+2*√2.
Вывод формулы для tg(α/2).
tg(α/2)=sin(α/2)/cos(α/2), cos(α)=cos²(α/2)-sin²(α/2), 1-cos(α)=sin²(α/2)+cos²(α/2)-((cos²(α/2)-sin²(α/2))=2*sin²(α/2), sin(α)=2*sin(α/2)*cos(α/2). Тогда (1-cos(α))/sin(α)=sin(α/2)/cos(α/2)=tg(α/2)
Вывод формулы для tg(α/2).
tg(α/2)=sin(α/2)/cos(α/2), cos(α)=cos²(α/2)-sin²(α/2), 1-cos(α)=sin²(α/2)+cos²(α/2)-((cos²(α/2)-sin²(α/2))=2*sin²(α/2), sin(α)=2*sin(α/2)*cos(α/2). Тогда (1-cos(α))/sin(α)=sin(α/2)/cos(α/2)=tg(α/2)
Ответ дал:
0
Потому что нет такой формулы. tg целого аргумента равен целому аргументу sin и cos.
Ответ дал:
0
Извините, но такая формула есть. Сейчас я добавлю в решение её вывод.
Ответ дал:
0
Добавил вывод формулы. Что скажете?
Ответ дал:
0
Извините, я нашел эту формулу. Спасибо за решение и объяснение.
Ответ дал:
0
Желаю удачи!
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад