Question

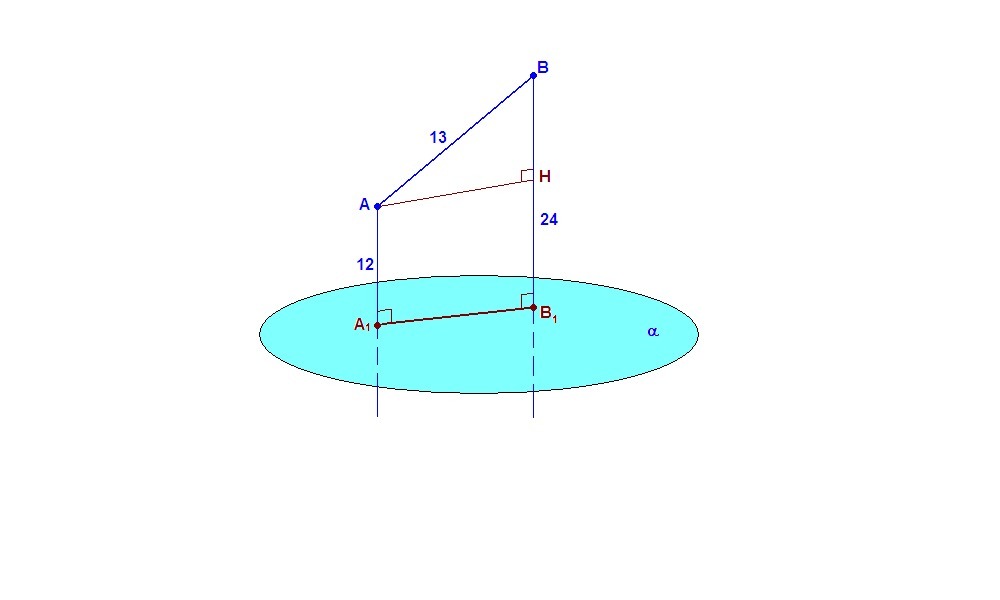
Отрезок AB не имеет общих точек с плоскостью альфа. Через точки A и B проведены прямые, перпендикулярные плоскости альфа и пересекающие её в точках A1 и B1 соответственно. Вычислите длину отрезка А1В1 если АВ = 13 СМ, АА1 = 12 см и ВВ1 = 24 см.

Answer 1

Так как АА₁⊥α и ВВ₁⊥α, то АА₁║ВВ₁.

Параллельные прямые задают плоскость, которая пересекает плоскость α по прямой А₁В₁ (так как эти точки принадлежат обеим плоскостям).

Итак, точки А, А₁, В₁, В лежат в одной плоскости, а четырехугольник АА₁В₁В - прямоугольная трапеция.

Проведем высоту АН. А₁АНВ₁ - прямоугольник, тогда НВ₁ = А₁А = 12 см,

АН = А₁В₁.

ВН = ВВ₁ - В₁Н = 24 - 12 = 12 см

ΔАВН: ∠АНВ = 90°, по теореме Пифагора

            АН = √(АВ² - ВН²) = √(169 - 144) = √25 = 5 см

А₁В₁ = АН = 5 см