Question

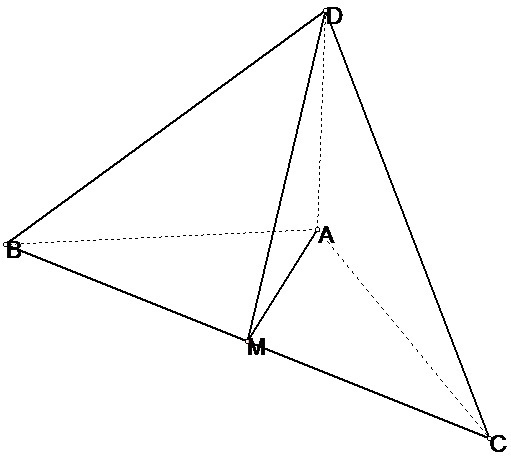
243. основанием пирамиды DABC является треугольник АВС,у которого АВ=АС=13 см,ВС=10см;ребро АD перпендикулярно к плоскости основания и равно 9 см. найдите площадь боковой поверхности пирамиды

Answer 1

Треугольники АВD и АСD прямоугольные, их площади равны по 1/2*13*9.
Треугольник ВСD- равнобедренный, его стороны СD и СВ раны,т.к. они имеют равные проекции на плоскость основания. Найдем высоту АМ в основании по теореме Пифагора.
АМ = √(13²-5²) = 12.
 DM=√(9²+12²)=15. Площадь треугольника ВСD равна 1/2*10*15.
Теперь складываем площади боковых граней: 2*1/2*13*9 + 1/2*10*15 = 
127+75 = 192 см².