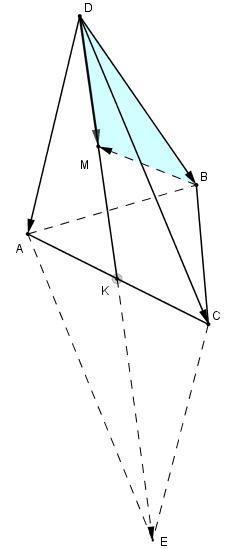
дан тетраэдр DABC, K-середина ребра AC, M-середина отрезка KD, вектор DA=вектору a, вектор DB=вектору b, вектор DC=вектору c. Разложите вектор BM по векторам a,b,c.
Ответы
Ответ дал:
0
Достроим до параллелограмма ADCE, так как K - середина АС, то по правилу параллелограмма
Так как M - середина DK, то
По правилу треугольника (из треугольника DMB)
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
11 лет назад