Question

Постройте график функции y=(х-1)(х^2-5х+6)/х-3 и определите,при каких значениях m прямая y=m имеет с графиком поровну одну общую точку.Заранее спасибо.

Answer 1

$y= frac{(x-1)(x^2-5x+6)}{x-3} \ x-3 neq 0 \ x neq 3$
Функция не определена в точке x=3

Решение квадратного уравнения $x^2-5x+6=0$
$x^2-5x+6=0 \ x_{1}+ x_{2} =5 \ x_{1} x_{2}=6 \ x_{1}=2 \ x_{2}=3$

$y= frac{(x-1)(x-2)(x-3)}{x-3} \ y=(x-1)(x-2) \ y=x^2-3x+2$

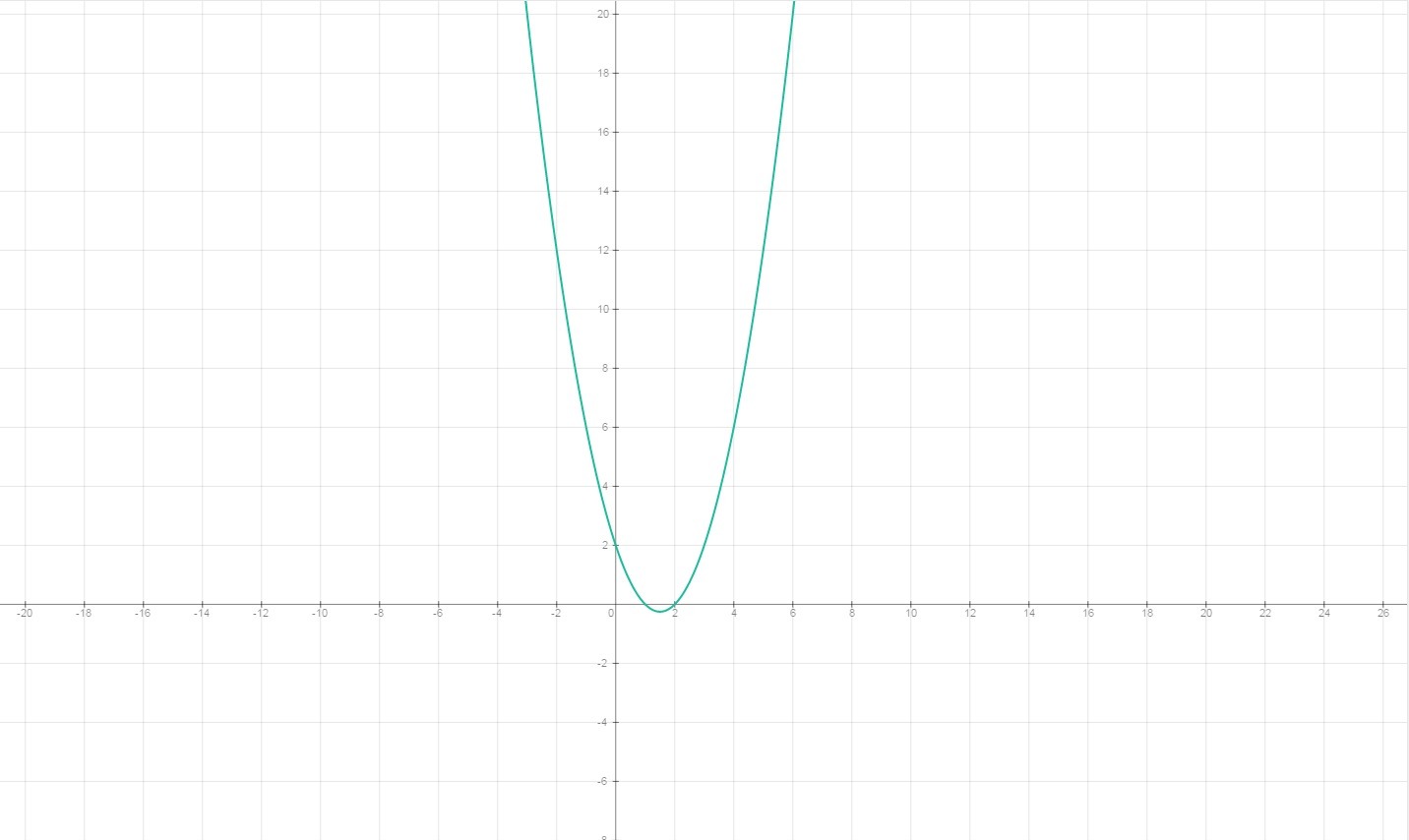
Выполняем построение графика функции.
Таблица точек:
x -3  -2  -1  0  1  2   3  4  5
y 20 12  6   2  0  0  2  6  12
(график прикреплен к решению как фото)

Теперь разберемся с прямой y=m. Это прямая, параллельная оси абцисс. Одна общая точка с графиком будет при прохождении прямой через вершину параболы, которой является наш график. Еще нам известно, что функция имеет разрыв в точке x=3, значит через этот разрыв можно провести еще одну прямую, имеющую с графиком одну общую точку.

Абциссу параболы находим по формуле
$x_{0}= frac{-b}{2a}$

$x_{0}= frac{3}{2}$ 
Теперь ордината

$y_{0}=( frac{3}{2})^2 -3* frac{3}{2}+2=- frac{1}{4}$

Первое решение найдено, теперь второе

$y=3^2-3*3+2=2$

Ответ: прямая y=m имеет с графиком одну общую точку при $m=- frac{1}{4}$ или $m=2$

Answer 2

Огромное спасибо!