На медиане МС равнобедренном треугольнике МРК с основанием РК отмечена точка В. Докажите, что
а) ∆МВК = ∆МВР;
б) ∆КВС = ∆МВС.
Ответы
Ответ дал:
0
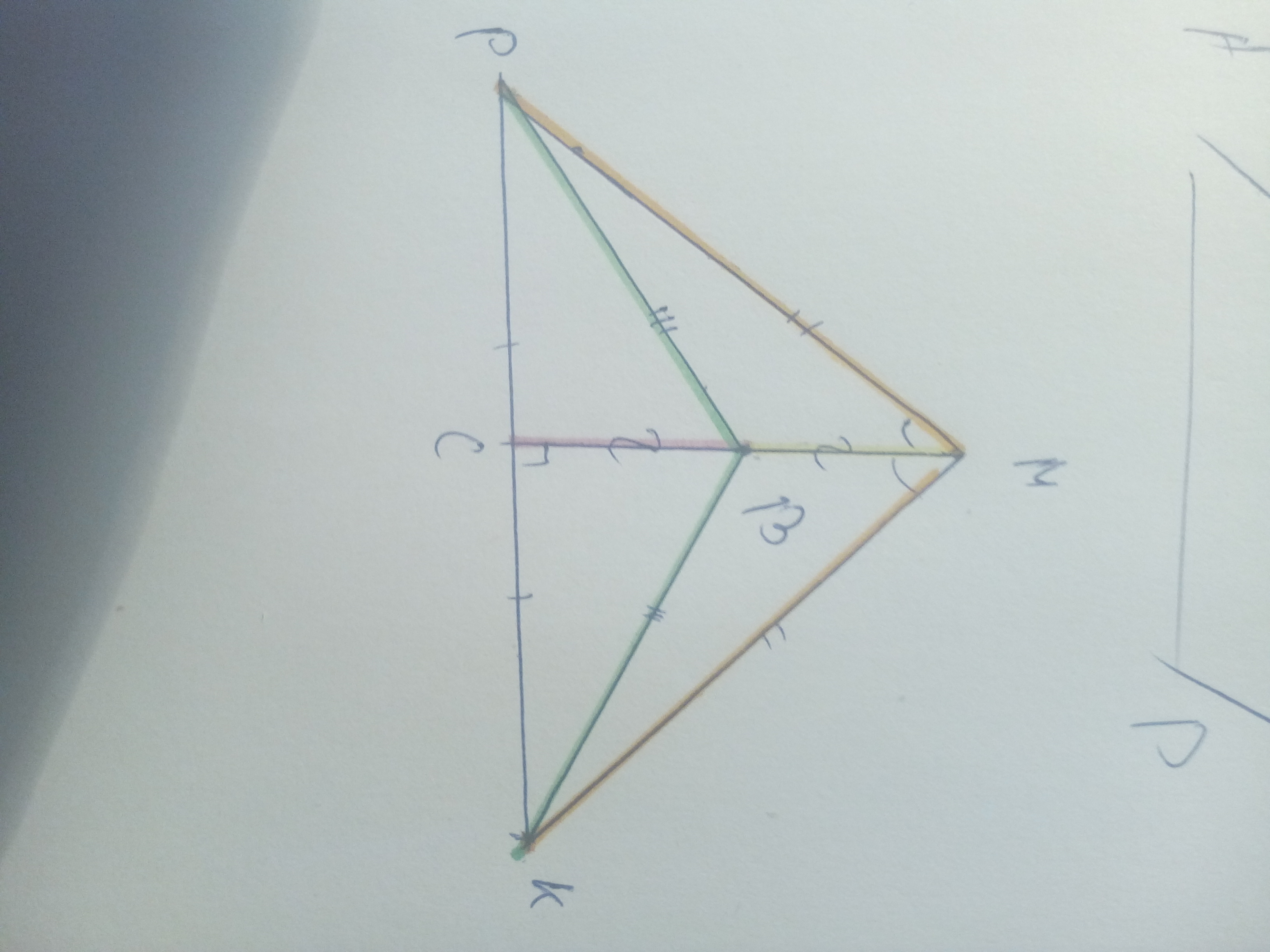
а) В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой, и высотой. Тогда ∠PMB = ∠KMB.
PM = MK - как боковые стороны.
BM - общая сторона.
Значит, ∆MBK = ∆MBP - по I признаку.
б) Т.к. MC - медиана, то PC = CК, а т.к. МС - и высота, то ∠PCM = ∠KCM = 90°.
BC - общая сторона.
Значит, ∆KBC = ∆PBC - по I признаку.
PM = MK - как боковые стороны.
BM - общая сторона.
Значит, ∆MBK = ∆MBP - по I признаку.
б) Т.к. MC - медиана, то PC = CК, а т.к. МС - и высота, то ∠PCM = ∠KCM = 90°.
BC - общая сторона.
Значит, ∆KBC = ∆PBC - по I признаку.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад