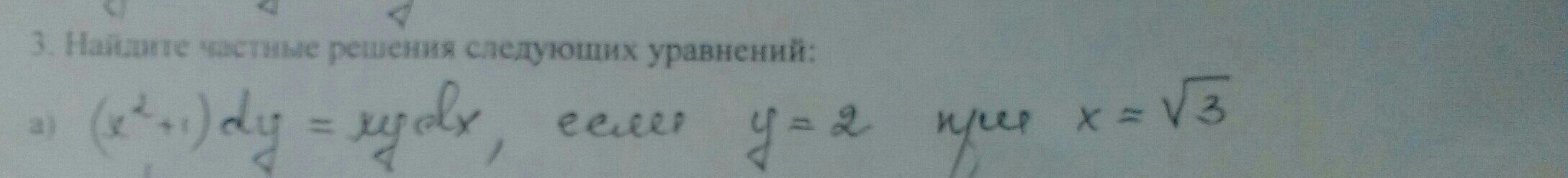Ответы
Ответ дал:
0
Итак, поделим уравнение на dy:
xyx'=1+x^2
Разрешим относительно старшей производной:
x'=(1+x^2)/xy
Разделяем переменные:
x'=(1+x^2)/x * (1/y)
Запишем x' в виде dx/dy:
dx/dy=(1+x^2)/x * (1/y)
Теперь сделаем так, чтоб слева остались только иксы, а слева игреки, т. е. разделим уравнение на (1+x^2)/x и умножим на y, получаем:
xdx/1+x^2=dy/y, ну и постоянное решение - x=0
Интегрируем обе части уравнения:
(в левой части x загоним под дифференциал и будем интегрировать по x^2)
1/2* ln(1+x^2)=ln|y| + lnС, здесь С можно записать как lnC, так как он будет всё равно пробегать все значения.
(1+x^2)^1/2=Cy,
Т. о. общее решение:
y=((1+x^2)^1/2)/C
y = 2; x = √3
2 = ((1 + (√3)^2)^1/2)/C
2 = ( (1 + 3)^1/2)/C
2 = (2/C)
C = 1
Частное решение
y = (1+x^2)^1/2
xyx'=1+x^2
Разрешим относительно старшей производной:
x'=(1+x^2)/xy
Разделяем переменные:
x'=(1+x^2)/x * (1/y)
Запишем x' в виде dx/dy:
dx/dy=(1+x^2)/x * (1/y)
Теперь сделаем так, чтоб слева остались только иксы, а слева игреки, т. е. разделим уравнение на (1+x^2)/x и умножим на y, получаем:
xdx/1+x^2=dy/y, ну и постоянное решение - x=0
Интегрируем обе части уравнения:
(в левой части x загоним под дифференциал и будем интегрировать по x^2)
1/2* ln(1+x^2)=ln|y| + lnС, здесь С можно записать как lnC, так как он будет всё равно пробегать все значения.
(1+x^2)^1/2=Cy,
Т. о. общее решение:
y=((1+x^2)^1/2)/C
y = 2; x = √3
2 = ((1 + (√3)^2)^1/2)/C
2 = ( (1 + 3)^1/2)/C
2 = (2/C)
C = 1
Частное решение
y = (1+x^2)^1/2
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад