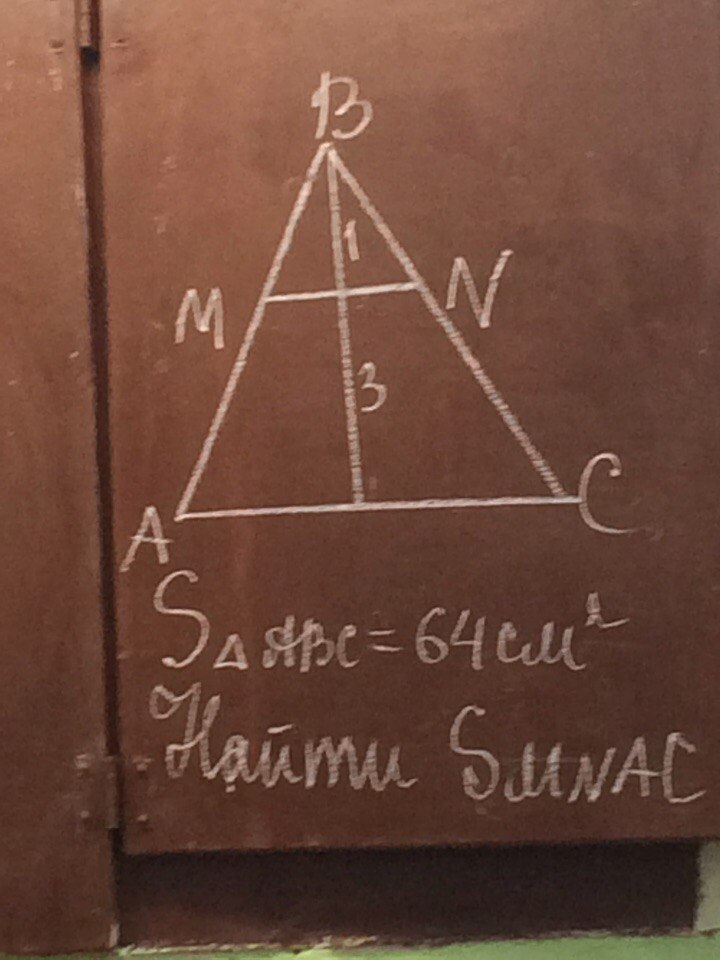Ответы
Ответ дал:
0
Рассматриваем ΔАВС и ΔМВN.
∠В - общий; ∠ВАС=∠ВМN - соответственные.
Следовательно ΔАВС подобен ΔМВN.
Коэффициент подобия , т. к. высота в ΔМВN равна h=1. а высота в ΔАВС - H=1+3=4
, т. к. высота в ΔМВN равна h=1. а высота в ΔАВС - H=1+3=4

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

S (ΔMBN)=S(ΔABC)*k²

S(MNCА)=S(ΔABC)-S(ΔMBN)=64-4=60
Ответ: S(MNAC)=60
∠В - общий; ∠ВАС=∠ВМN - соответственные.
Следовательно ΔАВС подобен ΔМВN.
Коэффициент подобия
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S (ΔMBN)=S(ΔABC)*k²
S(MNCА)=S(ΔABC)-S(ΔMBN)=64-4=60
Ответ: S(MNAC)=60
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад