натолкните на решение. сначала избавляюсь от степени у основания логарифма, далее сумма логарифмом как логарифм произведения, а дальше как бы избавиться от ab основания логарифма?
Приложения:
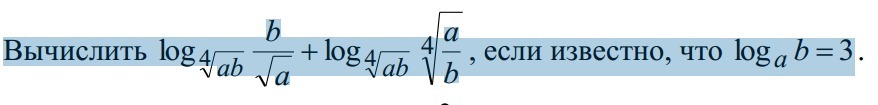
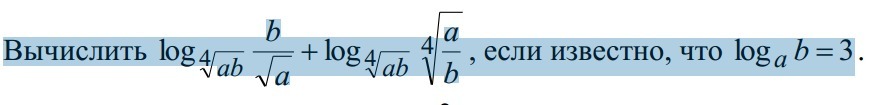
Ответы
Ответ дал:
0
Попробую
![log_{ sqrt[4]{ab} }( frac{b}{ sqrt{a} } )+log_{ sqrt[4]{ab} }(sqrt[4]{ frac{a}{b} } )=log_{ sqrt[4]{ab} }( frac{b}{ a^{1/2} }* frac{a^{1/4}}{b^{1/4}} )=log_{ sqrt[4]{ab} }( frac{b^{3/4}}{a^{1/4}} ) log_{ sqrt[4]{ab} }( frac{b}{ sqrt{a} } )+log_{ sqrt[4]{ab} }(sqrt[4]{ frac{a}{b} } )=log_{ sqrt[4]{ab} }( frac{b}{ a^{1/2} }* frac{a^{1/4}}{b^{1/4}} )=log_{ sqrt[4]{ab} }( frac{b^{3/4}}{a^{1/4}} )](https://tex.z-dn.net/?f=log_%7B+sqrt%5B4%5D%7Bab%7D+%7D%28+frac%7Bb%7D%7B+sqrt%7Ba%7D+%7D+%29%2Blog_%7B+sqrt%5B4%5D%7Bab%7D+%7D%28sqrt%5B4%5D%7B+frac%7Ba%7D%7Bb%7D+%7D+%29%3Dlog_%7B+sqrt%5B4%5D%7Bab%7D+%7D%28+frac%7Bb%7D%7B+a%5E%7B1%2F2%7D+%7D%2A+frac%7Ba%5E%7B1%2F4%7D%7D%7Bb%5E%7B1%2F4%7D%7D++%29%3Dlog_%7B+sqrt%5B4%5D%7Bab%7D+%7D%28+frac%7Bb%5E%7B3%2F4%7D%7D%7Ba%5E%7B1%2F4%7D%7D+%29)
Есть такое замечательное свойство логарифмов:
Причем новое основание с может быть любым, лишь бы > 0 и не = 1.
Перейдем в нашем примере к основанию а.
![log_{ sqrt[4]{ab} }( frac{b^{3/4}}{a^{1/4}} )= log_a( frac{b^{3/4}}{a^{1/4}} ):log_a(sqrt[4]{ab}) = frac{3/4*log_a(b)-1/4*log_a(a)}{1/4*(log_a(a)+log_a(b))} = log_{ sqrt[4]{ab} }( frac{b^{3/4}}{a^{1/4}} )= log_a( frac{b^{3/4}}{a^{1/4}} ):log_a(sqrt[4]{ab}) = frac{3/4*log_a(b)-1/4*log_a(a)}{1/4*(log_a(a)+log_a(b))} =](https://tex.z-dn.net/?f=log_%7B+sqrt%5B4%5D%7Bab%7D+%7D%28+frac%7Bb%5E%7B3%2F4%7D%7D%7Ba%5E%7B1%2F4%7D%7D+%29%3D+log_a%28+frac%7Bb%5E%7B3%2F4%7D%7D%7Ba%5E%7B1%2F4%7D%7D+%29%3Alog_a%28sqrt%5B4%5D%7Bab%7D%29+%3D+frac%7B3%2F4%2Alog_a%28b%29-1%2F4%2Alog_a%28a%29%7D%7B1%2F4%2A%28log_a%28a%29%2Blog_a%28b%29%29%7D+%3D)
Мы знаем, что , а
, а  подставляем
подставляем

Есть такое замечательное свойство логарифмов:
Причем новое основание с может быть любым, лишь бы > 0 и не = 1.
Перейдем в нашем примере к основанию а.
Мы знаем, что
Ответ дал:
0
спасибо большое!
Вас заинтересует
2 года назад
2 года назад
7 лет назад
10 лет назад