Гипотенуза прямоугольного треугольника равна 16.Найдите длину окружности ,описанной около этого треугольника
Ответы
Ответ дал:
0
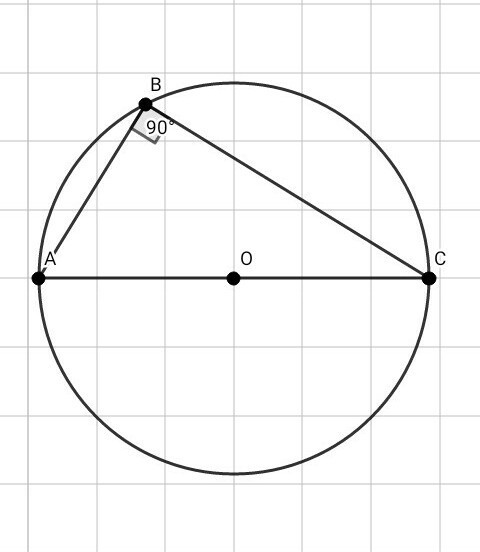
Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
Вписанный угол равен половине дуги, на которую этот угол опирается
угол АВС = 90° → U AC = 2 × угол АВС = 2 × 90° = 180°
Значит, АС = d — это диаметр окружности
Длина окружности вычисляется по формуле:
ОТВЕТ: L = 16π
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад