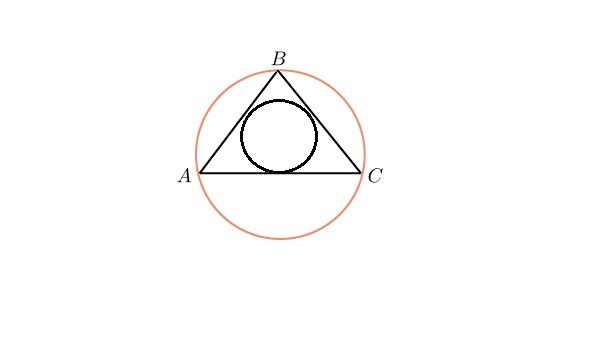
найдите площадь круга, описанного около правильного треугольника, и периметр треугольника, если радиус вписанного в этот треугольник круга равен 2 корня из 3 см. Сделайте чертеж.
Ответы
Ответ дал:
0
Для правильного треугольника радиус вписанной окружности вычисляется по формуле  , где а - сторона. Отсюда
, где а - сторона. Отсюда  .
.

Радиус описанной вокруг правильного треугольника окружности вычисляется следующим образом:
 .
.

Радиус описанной вокруг правильного треугольника окружности вычисляется следующим образом:
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад