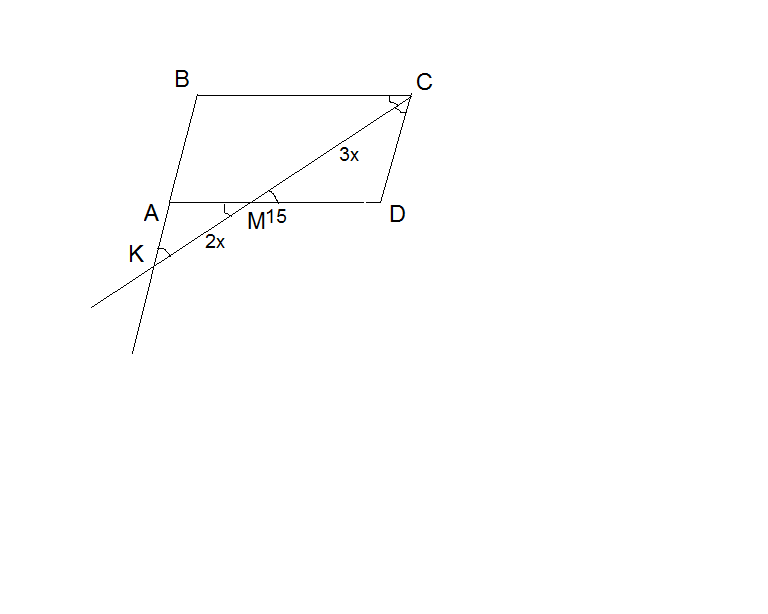
В параллелограмме ABCD биссектриса острого угла C пересекает сторону AD в точке M, а продолжение стороны AB в точке K, KM : MC = 2: 3. Найдите периметр параллелогоамма ABCD ,если AD=15 см.
Ответы
треугольник МДС равнобедренный угол СМД=уголМСВ как внутренние разносторонние =уголМСД. МД=СД
угол МСД=угол АКМ как внутренние разносторонние =уголАМК
треугольники АКД подобен треугольнику МСД по двум углам
КМ/СМ=АМ/МД, МД=а, АМ=15-а
2/3=15-а/а
а=9 = МД= СД
периметр = 15+15+9+9=48
1) Рассмотрим треугольник MDC.
Угол DMC = углу BCK (как накрест лежащие) = DCM ( так как CK - биссектриса угла C), значит треугольник MDC - равнобедренный, значит MD = DC.
2) Рассмотрим тругольники KAM и MCD.
Угол CMD = углу KMA (как вертикальные)
Угол MKA = углу MCD (как накрест лежащие)
Значит треугольник KAM и MCD - подобные ( по двум углам) , значит их стороны относятся как 2:3 (по условию), значит AM/MD = 2/3 = 6/9
3) MD = DC (п.1), значит периметр параллелограмма равен:
15+15+9+9 = 48 см
Ответ: Pabcd = 48 см