Ответы
Ответ дал:
0
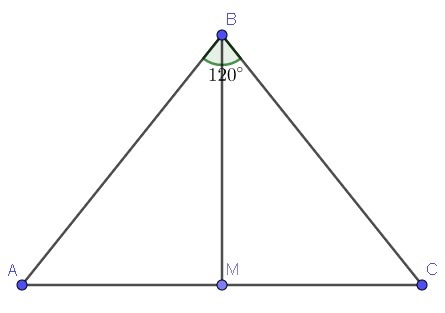
Поскольку BM - медиана и делит угол В пополам, то BM является биссектрисой. Если медиана треугольника является биссектрисой, то ΔABC - равнобедренный и BM является высотой.
Рассмотрим прямоугольный треугольник ABM в нём и
, тогда сторона АВ вычислим по определению синуса:
откуда выразим АВ:
см
Ответ: 8 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад