Question

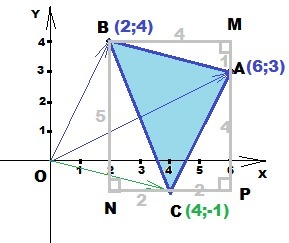
в декартовой системе координат даны точки А(6;3) и B(2;4). Точка С такова, что ОС=ОА-ОB. Найдите площадь треугольника АBC

Answer 1

A (6; 3); B (2; 4)

Так как точка О имеет координаты (0; 0), то координаты векторов ОА и ОВ равны координатам точек А и В соответственно.

$vec {OA}(6;3); vec {OB}(2,4)$

$vec {OC}=vec {OA}-vec {OB}=(6-2;3-4)=(4;-1)$

⇒ точка С имеет координаты (4; -1)

Площадь треугольника АВС можно вычислить как разность площади прямоугольника BMPN и угловых прямоугольных треугольников.

$S_{ABC}=S_{BMPN}-S_{BNC}-S_{APC}-S_{AMB}=\ \ =5*4-frac{5*2}{2} -frac{4*2}{2} -frac{4*1}{2} =20-5-4-2=9$

Ответ: С(4; -1); $S_{ABC}=9$ (кв.ед.)