Ответы
Ответ дал:
0
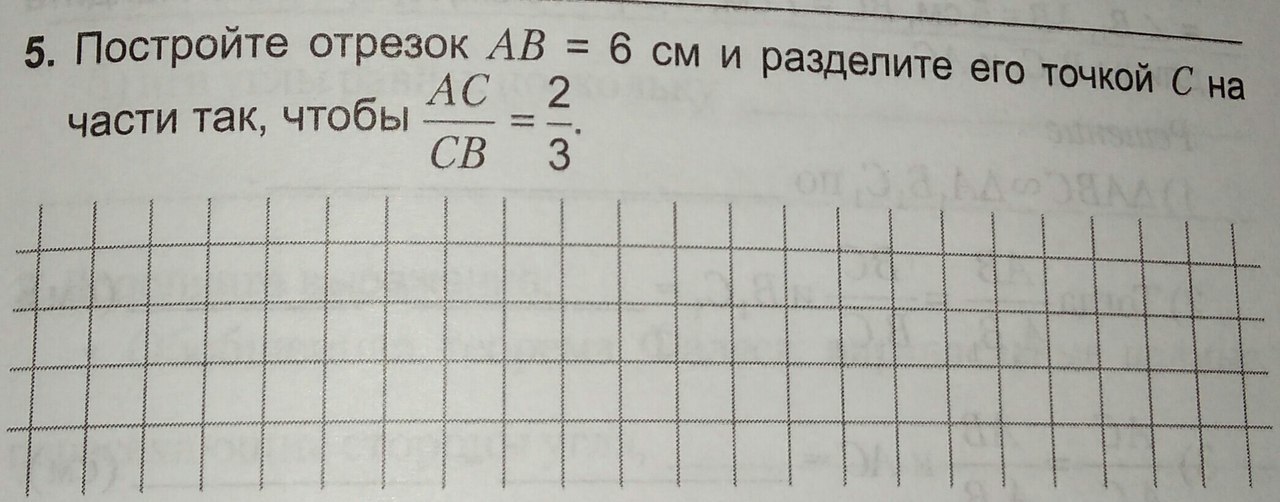
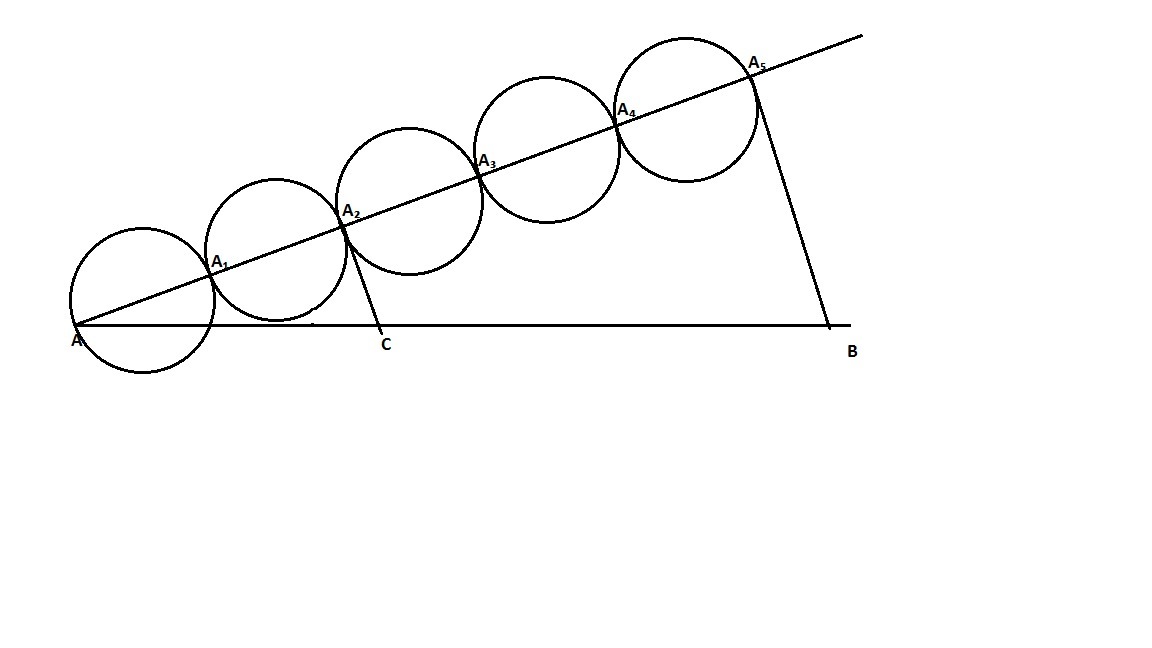
Строим прямую. На ней отмечаем точки А и В. Затем достраиваем эту прямую до угла. На второй стороне угла строим пять равных между собой окружности, касающихся друг друга внешним образом и радиусы которых лежат на второй стороне угла.
Затем через конец последней окружности (через точку А₅) проводим прямую, пересекающую первую прямую в точке B.
Потом строим прямую, проходящую через точку А₂, параллельно прямой А₅B.
Чтобы доказать, что , рассмотрим ΔАA₂C и ΔAA₅B.
, рассмотрим ΔАA₂C и ΔAA₅B.
Т.к. A₂C || A₅B, то ∠АA₂C = ∠AA₅B - как соответственные.
∠A₅AB - общий.
Значит, ΔАA₂C ~ ΔAA₅B - по I признаку.
Из подобия треугольников ⇒ .
.
Но Тогда
Тогда  , т.е.
, т.е. 
Затем через конец последней окружности (через точку А₅) проводим прямую, пересекающую первую прямую в точке B.
Потом строим прямую, проходящую через точку А₂, параллельно прямой А₅B.
Чтобы доказать, что
Т.к. A₂C || A₅B, то ∠АA₂C = ∠AA₅B - как соответственные.
∠A₅AB - общий.
Значит, ΔАA₂C ~ ΔAA₅B - по I признаку.
Из подобия треугольников ⇒
Но
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад