Question

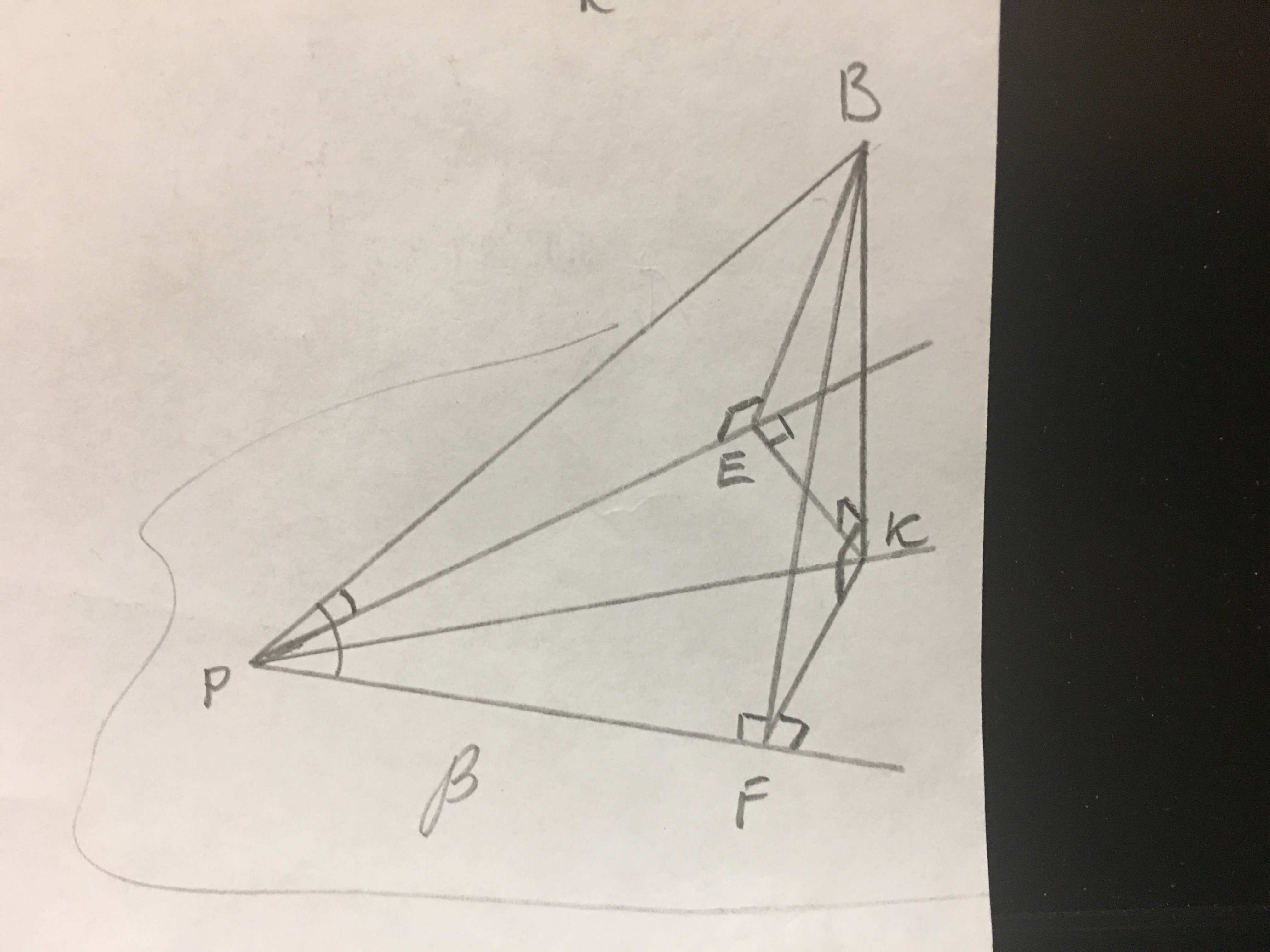
К плоскости b проведена наклонная BP (P принадлежит плоскости b), которая образует равные углы с прямыми PE и PF, лежащими в плоскости b. Докажите, что углы, образованные прямыми PE и PF с проекцией наклонной BP на плоскость b, равны.
Прошу решить подробно, обязательно с ЧЕРТЕЖОМ, если вы не хотите делать чертеж, то пожалуйста, не приступайте к решению.

Answer 1

∠ВРЕ=∠ВРF.
ВК⊥РК, РК∈β, значит РК - проекция наклонной ВР на плоскость β.
Прямоугольные тр-ки ВРЕ и ВРF равны т.к. острые углы равны и сторона ВР общая, значит РЕ=PF.
ВК⊥КЕ, ВК⊥РЕ ⇒ КЕ⊥РЕ. Аналогично KF⊥PF.
Прямоугольные тр-ки РKЕ и РKF равны по общей гипотенузе и катетам РЕ=PF, значит ∠КРЕ=КРF. 
Доказано.