от точки A окружности проведены две хорды AB и AC, длины которых равны радиусу. Точки B и C соединены отрезком. Найдите расстояние от центра окружности до хорды BC, если радиус равен 12 см. Только решите 100% вместе с "дано" "формулой" и "решением"
Ответы
Ответ дал:
0
АВ=АС=R=12 см, ОК⊥ ВС.
ОК=?.
В четырёхугольнике все стороны равны (радиусу), значит АВОС - ромб.
Диагональ ромба ОА=R.
Диагонали ромба перпендикулярны и в точке пересечения делятся пополам.
ОК=АО/2=R/2=12/2=6 см - это ответ.
ОК=?.
В четырёхугольнике все стороны равны (радиусу), значит АВОС - ромб.
Диагональ ромба ОА=R.
Диагонали ромба перпендикулярны и в точке пересечения делятся пополам.
ОК=АО/2=R/2=12/2=6 см - это ответ.
Приложения:
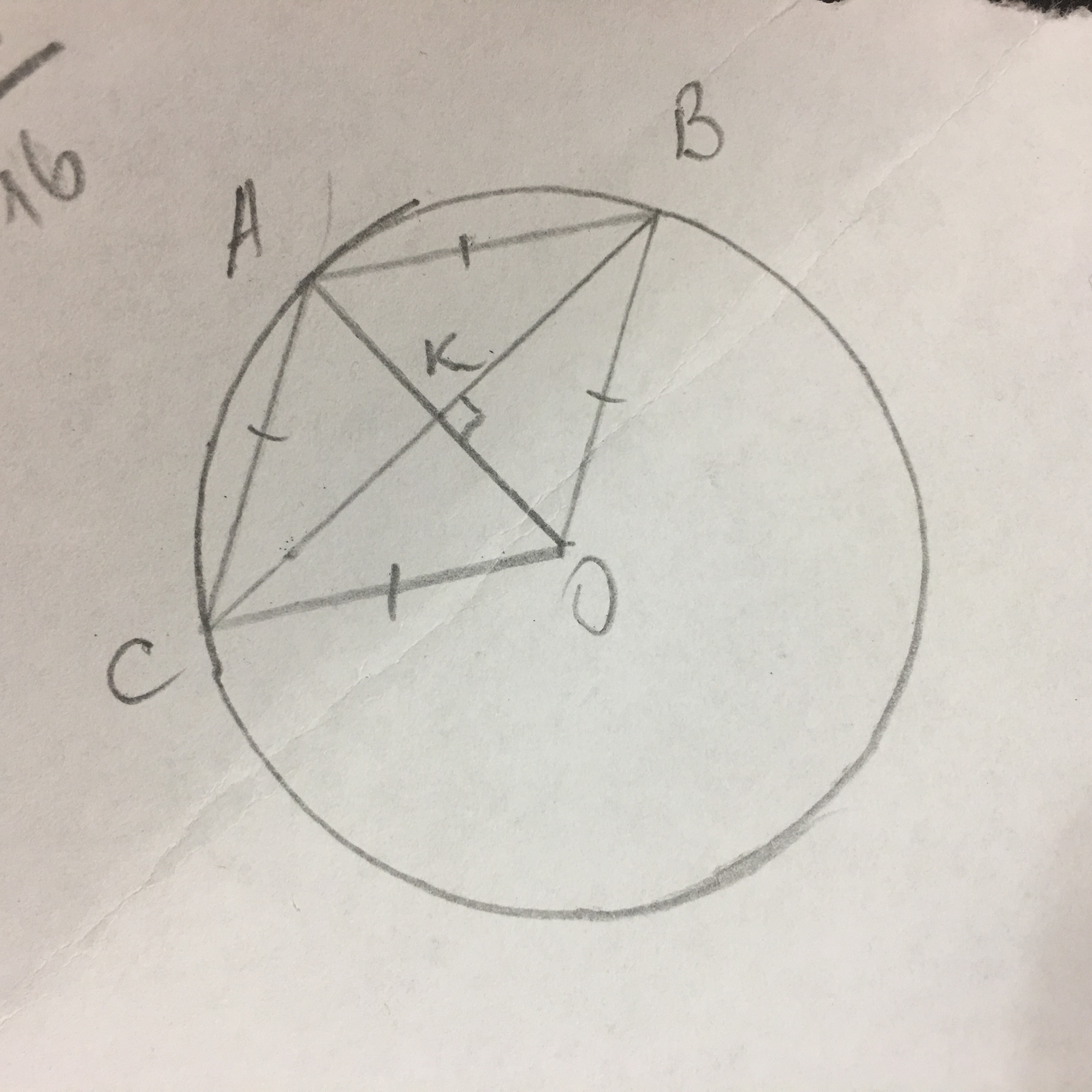
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад