Помогите пожалуйста решить уравнение , не понимаю какие преобразования нужно сделать.
Приложения:
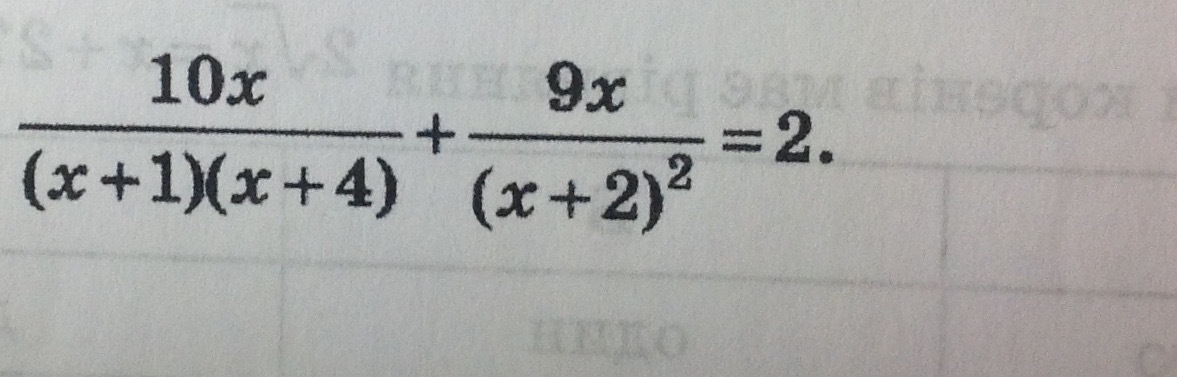
Ответы
Ответ дал:
0
ОДЗ:
Домножим обе части уравнения на
Разделим обе части уравнения на
Пусть
Вычислим дискриминант квадратного уравнения:
Поскольку
Обратная замена:
Найдем корни по формулам:
По т. Виета:
Ответ:
Ответ дал:
0
Ответ ответ ответ ответ ответ ответ
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад