Ответы
Ответ дал:
0
Всего 4 целочисленных решения
Ответ дал:
0
представим в виде

разделим на корень из 10, получим

оба корня должны быть целыми числами, значит x и y должны быть вида

подставляя в уравнение, получим

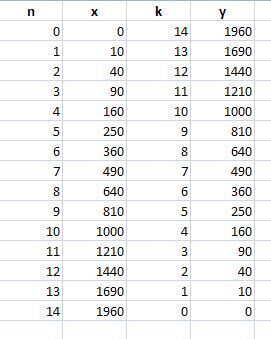
значения n и k могут быть такими:
n k
0 14
1 13
2 12
......................
13 1
14 0
соответственно x и y получаются возведением в квадрат и умножением на 10
ответ в иллюстрации
разделим на корень из 10, получим
оба корня должны быть целыми числами, значит x и y должны быть вида
подставляя в уравнение, получим
значения n и k могут быть такими:
n k
0 14
1 13
2 12
......................
13 1
14 0
соответственно x и y получаются возведением в квадрат и умножением на 10
ответ в иллюстрации
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад