Составить рекуррентную формулу для следующего ряда. Я пробовал решать (рисунок 2), но запутался. Объясните, как составить рекуррентную формулу для данного ряда. Заранее благодарен!
Приложения:
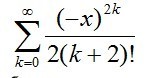

Ответы
Ответ дал:
0
для получения рекуррентной формулы нужно выразить член ряда через предыдущие (и, возможно, номер)



теперь возьмем член с k=1

отсюда

подставляя, получим

это и есть рекуррентная формула
теперь возьмем член с k=1
отсюда
подставляя, получим
это и есть рекуррентная формула
Вас заинтересует
2 года назад
7 лет назад
9 лет назад