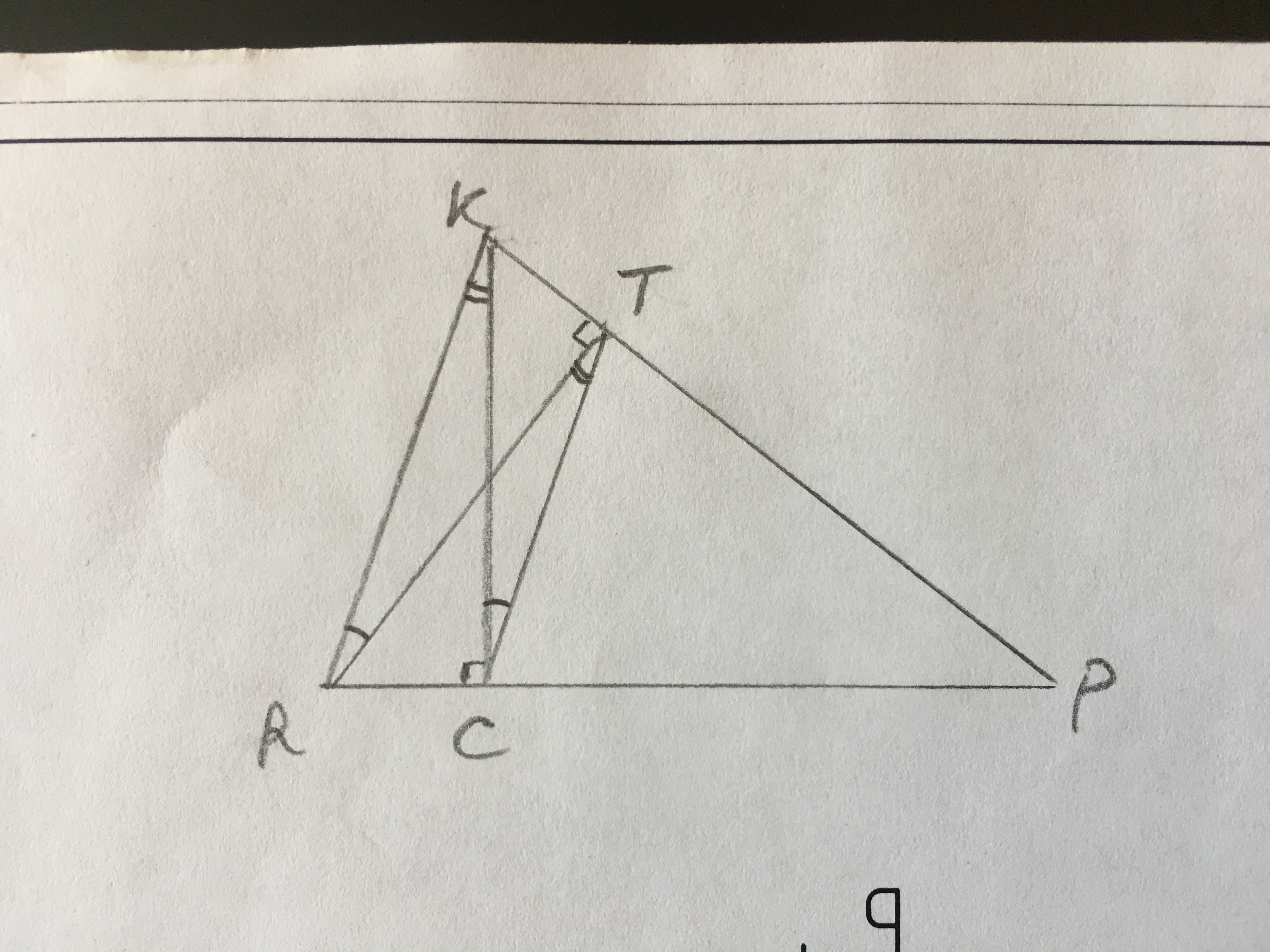
в остроугольном треугольнике RKP провели высоты RT и KC докажите что треугольники KPR и CTP подобны
Ответы
Ответ дал:
0
Прямоугольные треугольники RKC и RКТ имеют общую гипотенузу, значит вокруг четырёхугольника RКТС можно описать окружность с диаметром RK.
∠КRT=∠KCT т.к. они опираются на одну дугу KT.
В прямоугольном треугольнике RКТ ∠RКТ=90-∠КRT.
∠TCP=180-∠RCK-∠KCT=90-∠KRT=∠RКТ.
Аналогично ∠СТР=∠КRC.
В треугольниках RKP и СТР найдены две пары равных углов и угол Р - общий, значит треугольники подобны.
∠КRT=∠KCT т.к. они опираются на одну дугу KT.
В прямоугольном треугольнике RКТ ∠RКТ=90-∠КRT.
∠TCP=180-∠RCK-∠KCT=90-∠KRT=∠RКТ.
Аналогично ∠СТР=∠КRC.
В треугольниках RKP и СТР найдены две пары равных углов и угол Р - общий, значит треугольники подобны.
Приложения:
Ответ дал:
0
а признака подобия по трем углам вроде нет
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад