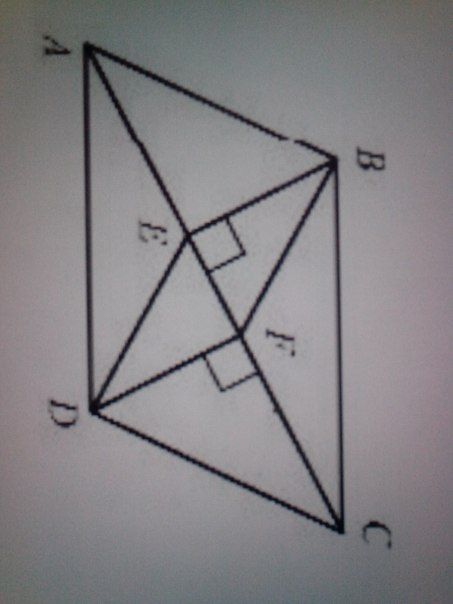
В параллелограмме ABCD проведены перпендикуляры BE и DF к диагонали AC. Докажите , что BFDE - параллелограмм.
Приложения:
Ответы
Ответ дал:
0
Т.к. к одной прямой АС проведены 2 перпендикуляра, значит эти перпендикуляры между собой параллельны: ВЕ || DF.
Площадь треугольника АВС=АС*ВЕ/2
Площадь треугольника АДС=АС*DF/2
Но эти площади равны между собой, т.к. диагональ параллелограмма делит его на 2 равных треугольника, т.е. ВЕ=DF
Т.к. ВЕ || DF и ВЕ=DF, значит ВFDE - параллелограмм
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад