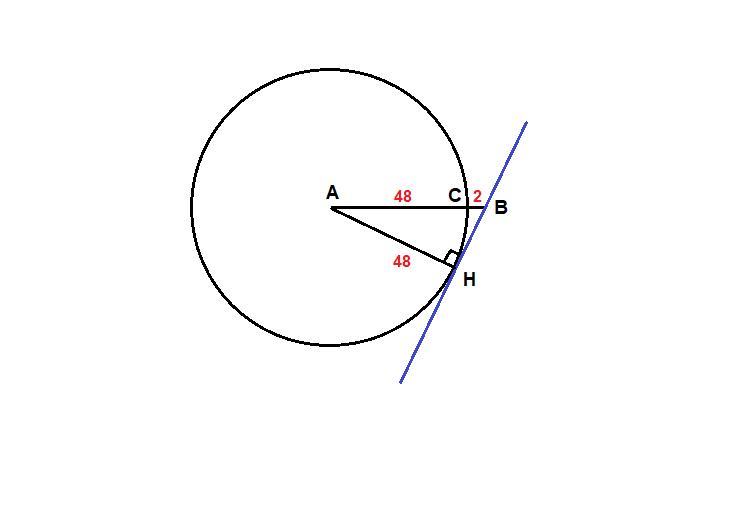
На отрезке AB выбрана точка C так, что AC=48 и BC=2. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Ответы
Ответ дал:
0
Ответ: 14
Объяснение:
ВН - касательная, Н - точка касания.
Проведем АН. АН⊥ВН как радиус, проведенный в точку касания.
АН = АС = 48
АВ = АС + СВ = 48 + 2 = 50
ΔАНС: ∠АНС = 90°, по теореме Пифагора
ВН = √(АВ² - АН²) = √(50² - 48²) = √((50 - 48)(50 + 48)) =
= √(2 · 98) = √(2 · 2 · 49) = 2 · 7 = 14
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад