Question

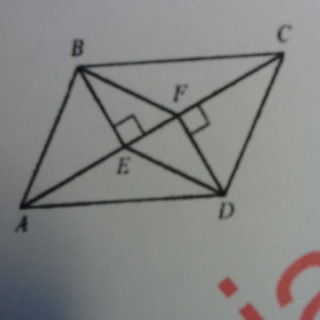
В параллелограмме ABCD проведены перпендикуляры ВЕ и DF к диагонали АС.Докажите,что треугольники BEF и DFE равны.Заранее спасибо

Answer 1

Если коротко, то: тр.BEF=тр.DFE по стороне и прилежащим к ней углам (EF-общая строна; уголЕ1=Е2, уголF1=F2)

Answer 2

Т.к.ВЕ и FД перпендикулярны АС, то они параллельны между собой.

S(ABC)=ВЕ*АС/2, а S(ACД)=ДЕ*АС/2. Но эти треугольники АВС и АСД равные, значит площади их равны. Тогда ВЕ=ДЕ. Сторона ЕF общая. Углы ВЕF и ДFЕ=90. Тогда треугольники ВЕF и ДЕF равны по 2-м равным сторонам и углу между ними