Question

pojalusta pomogite 56 zadanje srocnoo

Answer 1

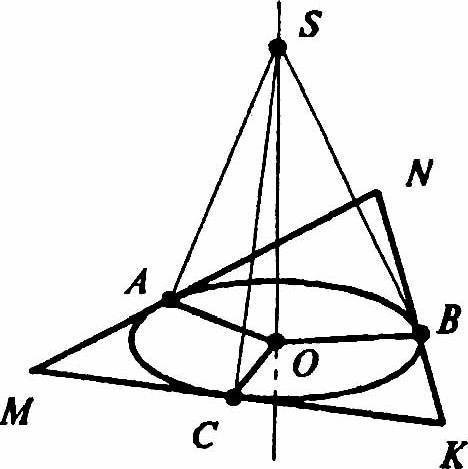
Допустим O - это центр вписанной окружности, а OS - данный перпендикуляр, тогда радиус будет равен:
r = АО = ОВ = ОС = 0,7 м., где точки А,В,С — точки касания сторон треугольника с окружностью.
Из теоремы о трех перпендикулярах SA ⊥ MN.
Отсюда по теореме Пифагора в ΔAOS найдем SA:
SA²=SO²+AO²
SA²=2.4²+0.7²=6.25
SA=√6.25=2.5 (м)
Ответ: В