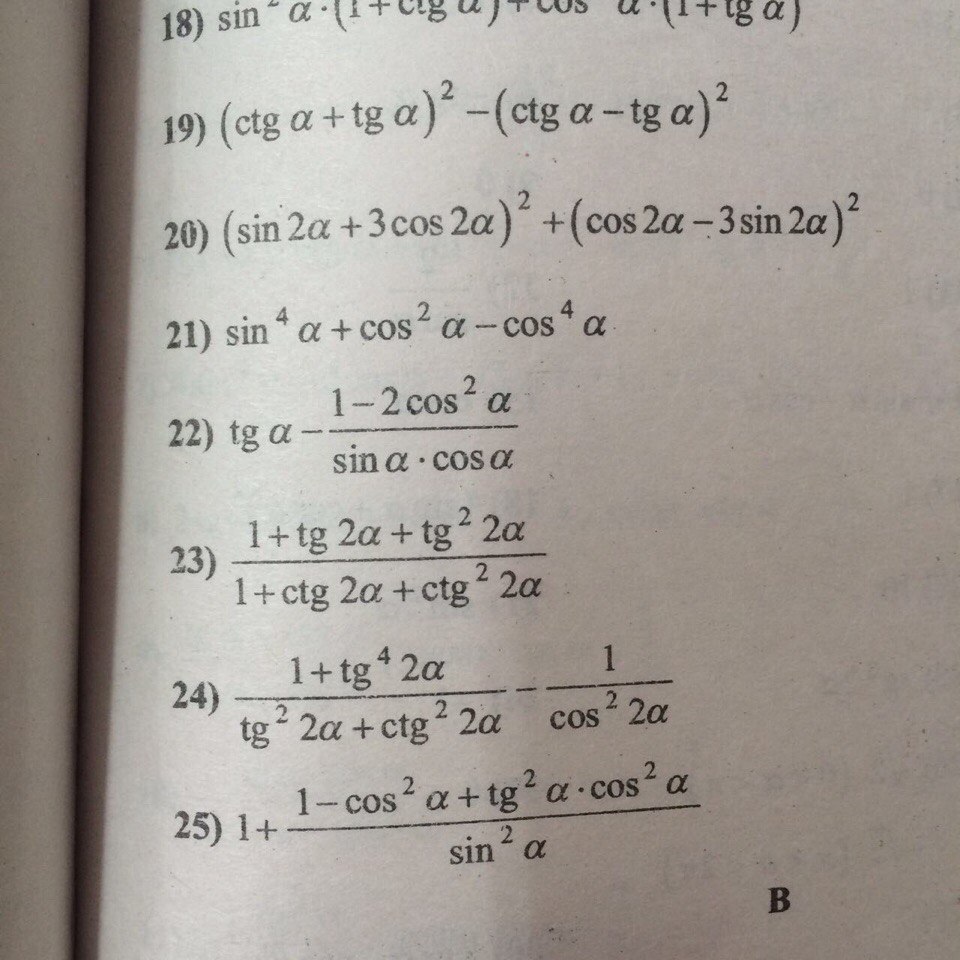Question

Тригонометрия 9 класс.23,25.Помогите,пожалуйста! !!СРОЧНО

Answer 1

23) Для удобства заменим tg 2α = x, ctg 2α = 1/x.
      (1+x+x²)/(1+(1/x)+(1/x²).
      Приведём в знаменателе к общему знаменателю:
      (1+x+x²)/((1+x+x²)/(x²)) = x² = tg² 2α.

25) Замена по частям: 1-cos²α = sin²α,
      tg²α*cos²α = (sin²α/cos²α)*cos²α = sin²α.
      Получаем (sin²α+sin²α)/sin²α = 2.
      

Answer 2

Спасибо больше, извините,не могли бы вы помочь с 24?

Answer 3

В 24 в левой дроби заменить tg^2(2a) на 1/(tg^2(2a)) и привести в знаменателе к общему знаменателю. После сокращения там будет tg^2(2a). который разложить на sin/cos и добавить правую дробь. Получим -1.