Question

Найдите сторону квадрата, вписанного в окружность радиусом 32 в корне

Answer 1

Ответ:

  8

Объяснение:

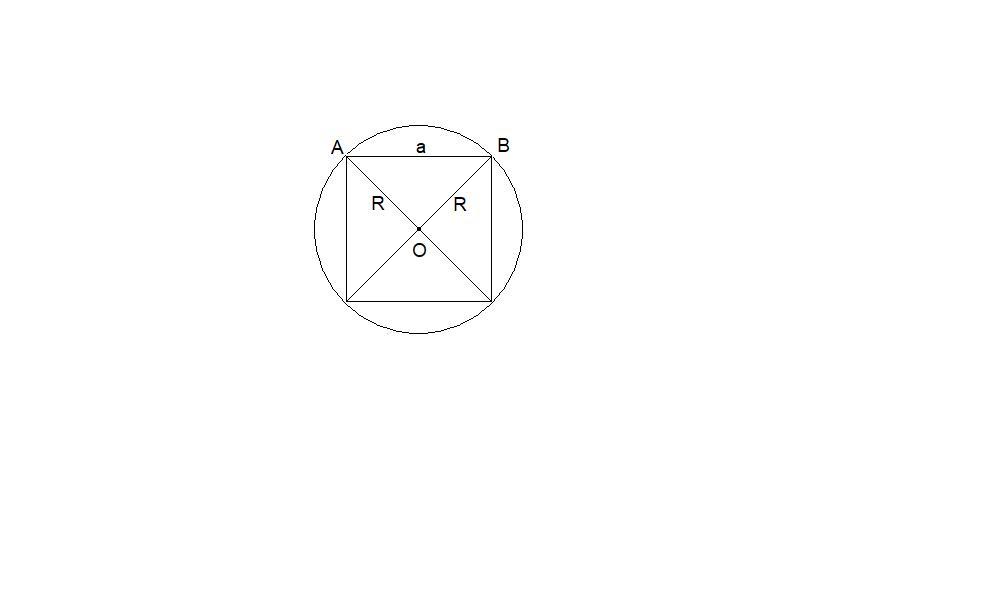
Диагонали квадрата перпендикулярны, равны и точкой пересечения делятся пополам.

Центр описанной окружности находится в точке пересечения диагоналей.

Тогда треугольник АОВ прямоугольный, равнобедренный.

a² = R² + R²

a² = 2R²

a = R√2 = √32 · √2 = √64 = 8