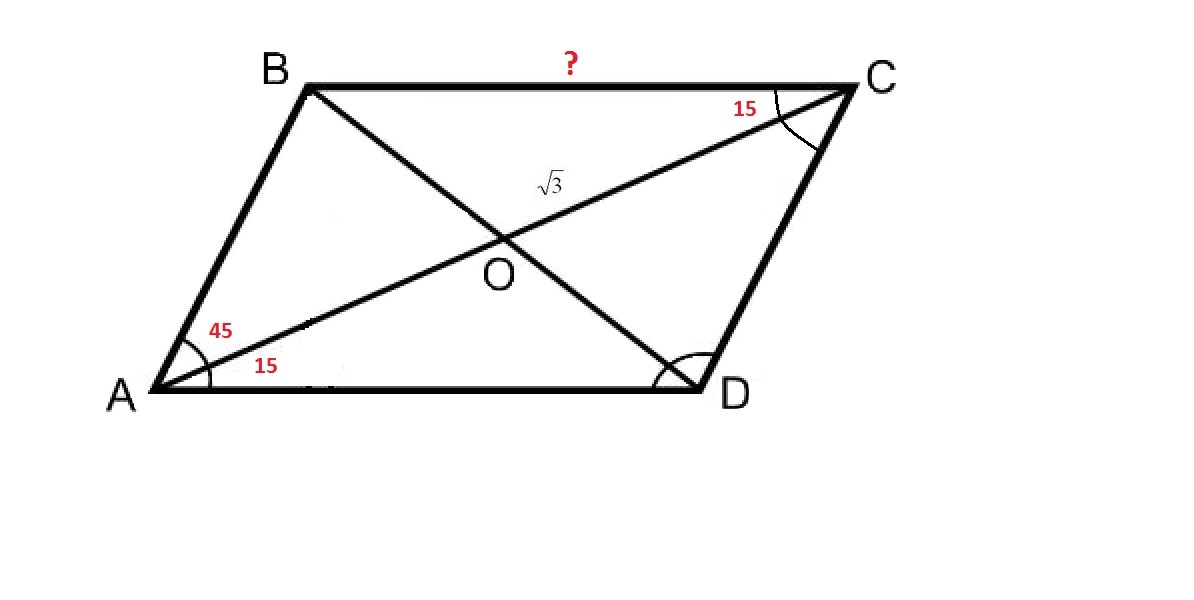
Большая диагональ параллелограмма равна корень из 3 и образует со сторонами углы которые равняются соответственно 15 и 45 градусов. Найдите большую сторону параллелограмма.
Ответы
Ответ дал:
0
Δ
В треугольнике против большего угла лежит большая сторона.
Значит будем искать сторону BC
по теореме синусов:
Ответ:
чертеж находится в приложении
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад