Дана правильная четырехугольная пирамида MABCD ,все ребра основания которой равны 6. Угол между прямыми DM и AL, L-середина ребра MB, равен 60. Найдите высоту пирамиды.
Решение поподробней если можно.
Спасибо!
Ответы
Пусть H - середина ABCD, MH - высота MABCD,
MH - медиана, биссектриса и высоты треугольника DBM => H - середина DB=> HL - средняя линия треугольника DMB => 2LH=DH;
AH перп. BD ( как диагонали квадрата),
AH перп МH ( т.к. МH - высота пирамиды)
DB пересекает MH в точке H => AH перп к плоскости DMB, значит угол HLA = 60 (из условия),
CA = √(CB^2+AB^2)=6√2 (по т.Пифагора)
HA=1/2CA=3√2
LM=AH/tg60= √6
DM=2LM=2√6
MH=√(DM^2-DH^2)=√6 (по т.Пифагора)
Ответ: √6
Здесь задача на непересекающиеся прямые.
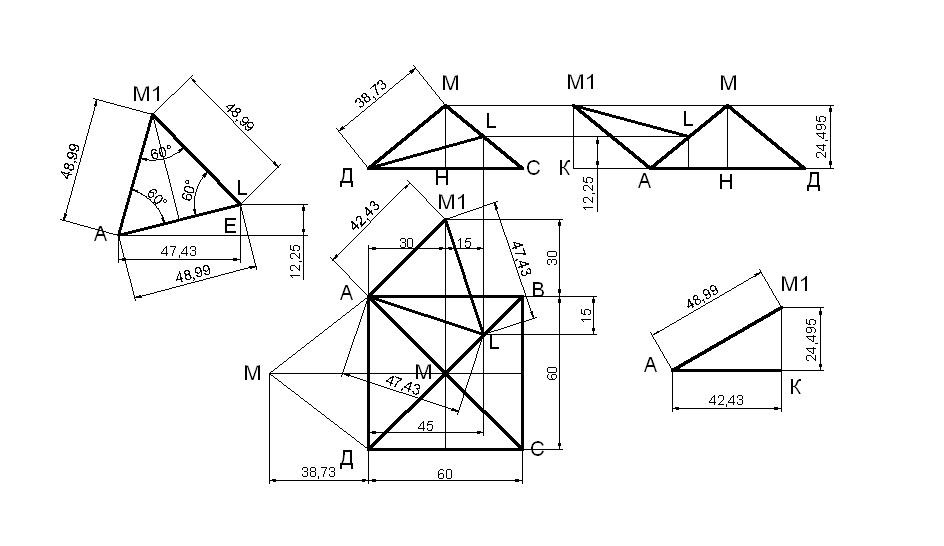
Чтобы обозначить угол в 60 градусов между прямыми DM и AL, L-середина ребра MB, надо сделать параллельный перенос ребра DM в точку А.
Из рисунка (см. вложение) видно, что получается равносторонний треугольник.
Точка L находится на половине высоты.
Отсюда вытекает уравнение AM1 = AL (размеры в мм, если сторона основания в см, то результат уменьшить в 10 раз).
(45^2 + 15^2) + (H/2)^2 = (30^2 + 30^2) + H^2
H = V((4/3)*(2250 - 1800)) = V600 = 24,495.