Question

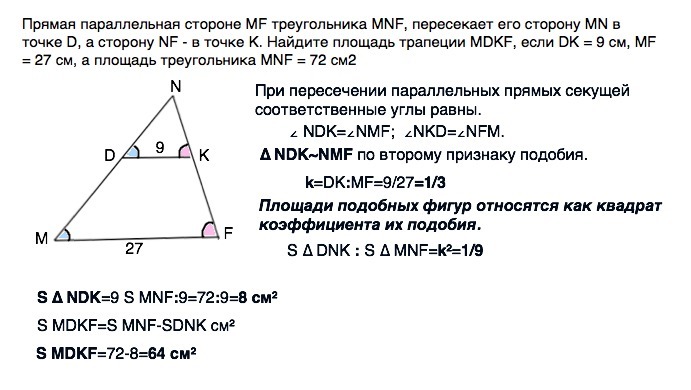
даю 50 баллов, Прямая параллельная стороне MF треугольника MNF, пересекает его сторону MN в точке D, а сторону NF - в точке K. Найдите площадь трапеции MDKF, если DK = 9 см, MF = 27 см, а площадь треугольника MNF = 72 см2

Answer 1

При пересечении параллельных прямых секущей соответственные углы равны. 

∠ NDK=∠NMF;  ∠NKD=∠NFM. 

∆ NDK~NMF по второму признаку подобия. 

k=DK:MF=9/27=1/3

Площади подобных фигур относятся как квадрат коэффициента их подобия. 

S ∆ DNK : S ∆ MNF=k²=1/9

S ∆ NDK=9 S MNF:9=72:9=8 см²

S MDKF=S MNF-SDNK см²

S MDKF=72-8=64 см²