Ответы
Ответ дал:
0
(5x - 9)² ≥ (9x - 5)²,
25х² - 90х + 81 ≥ 81х² - 90х +25,
25х² - 90х + 81 - 81х² + 90х - 25 ≥ 0,
-56х² + 56 ≥ 0,
х² - 1 ≤ 0,
(х - 1)(х + 1) ≤ 0.
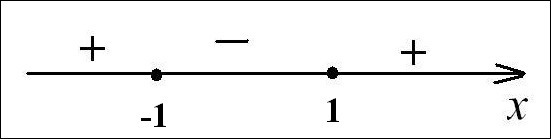
Рассмотрим функцию у = (х - 1)(х + 1) и найдем интервалы, на которых данная функция принимает значения у ≤ 0. Решим неравенство методом интервалов.
Нули функции: -1 и 1.
х ∈ [-1; 1].
Ответ: [-1; 1].
Приложения:
Ответ дал:
0
В левой части уравнения применим формулу разность квадратов
Последнее неравенство эквивалентно двойному неравенству
Ответ: x ∈ [-1;1]
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад