ДАЮ 40 БАЛЛОВ. СРООЧННОО
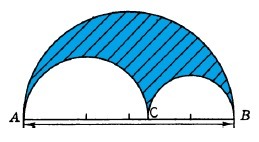
На отрезке AB равном 14 см как на диаметре построена полуокружность. Точка C лежит на отрезке AB. Определите длину границы выделенной фигуры, если AC и BC – диаметры полуокружностей.
Приложения:
Ответы
Ответ дал:
0
Длина окружности С=2πR, значит длина полуокружности с=С/2=πR.
АС+ВС=АВ.
Пусть радиус R - радиус большой полуокружности а r1 и r2 - радиусы малых полуокружностей. r1+r2=R.
Длина дуги АВ: ∪АВ=πR.
∪AC=πr1, ∪BC=πr2.
Сумма всех дуг:
Р=πR+πr1+πr2=π(R+r1+r2)=π(R+R)=2πR=πD=АВ·π=14π - это ответ.
АС+ВС=АВ.
Пусть радиус R - радиус большой полуокружности а r1 и r2 - радиусы малых полуокружностей. r1+r2=R.
Длина дуги АВ: ∪АВ=πR.
∪AC=πr1, ∪BC=πr2.
Сумма всех дуг:
Р=πR+πr1+πr2=π(R+r1+r2)=π(R+R)=2πR=πD=АВ·π=14π - это ответ.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад