Question

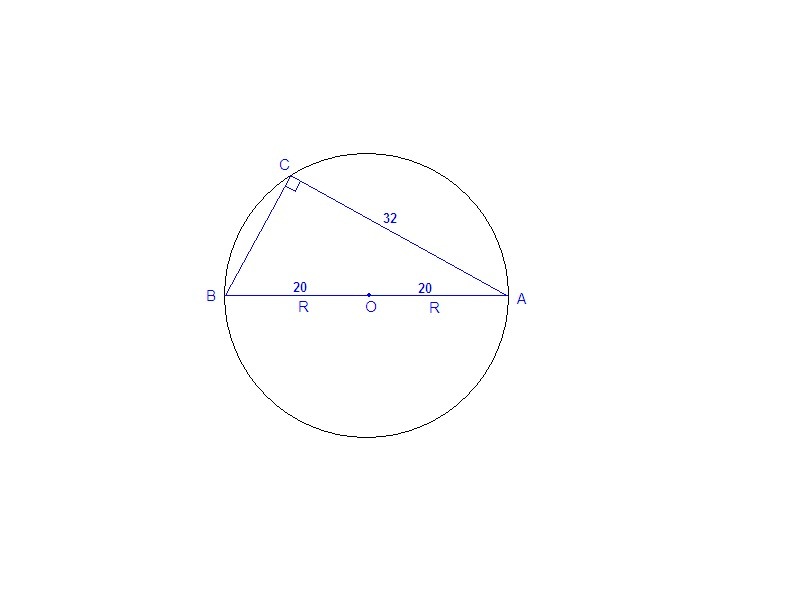
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.

Answer 1

Все вершины треугольника лежат на описанной окружности.

Если центр описанной окружности лежит на стороне треугольника, то эта сторона является диаметром окружности. Значит противоположный угол опирается на полуокружность, он вписанный и поэтому равен половине дуги, на которую опирается, т.е. 90°, ⇒

ΔАВС прямоугольный, АВ = 2R = 2 · 20 = 40.

По теореме Пифагора:

ВС = √(АВ² - АС²) = √(40² - 32²) = √((40 - 32)(40 + 32)) = √(8 · 72) =

= √(2 · 4 · 2 · 36) = 2 · 2 · 6 = 24