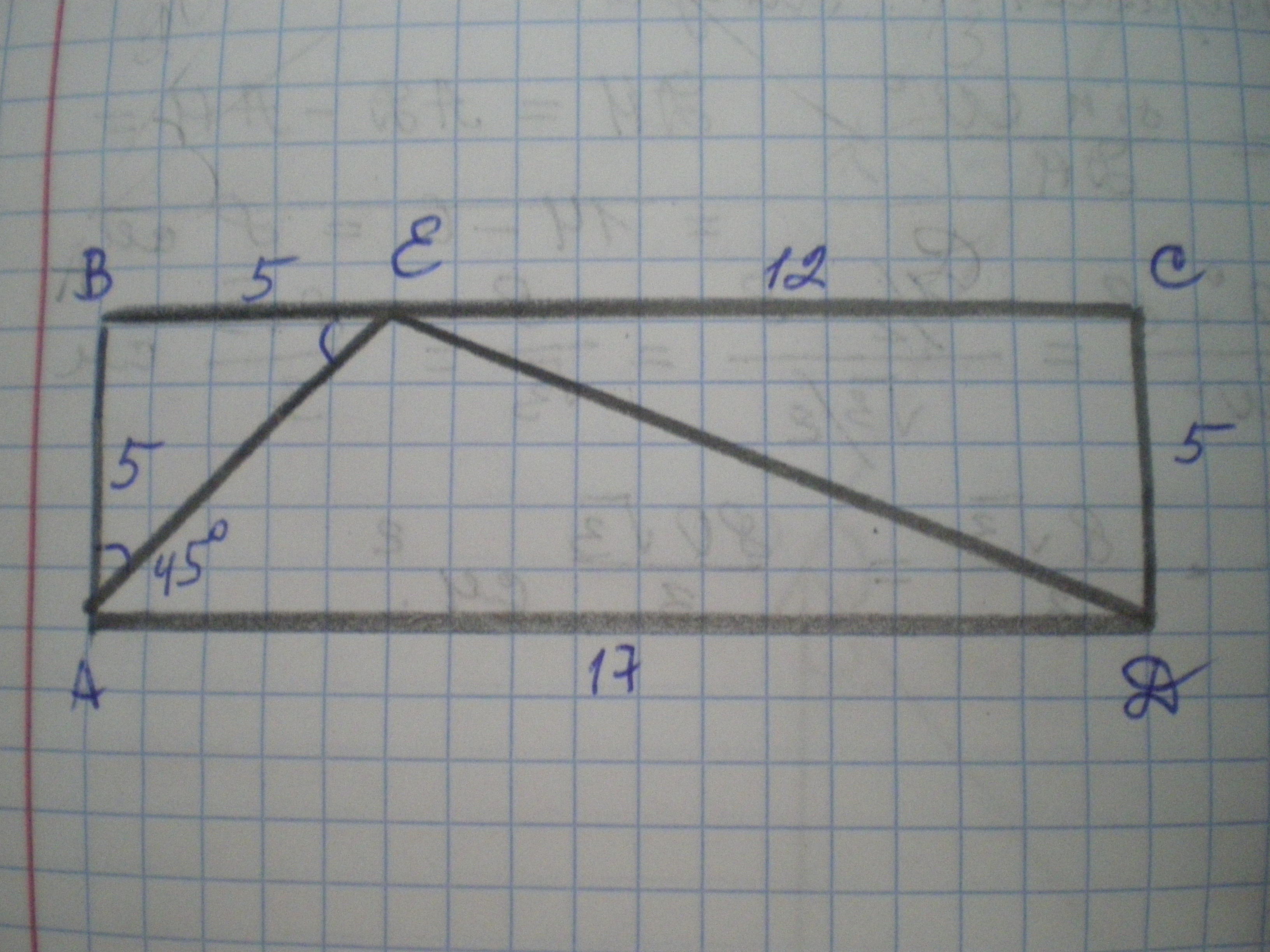
На стороне BC прямоугольника ABCD, у которого AB = 5 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
Ответы
Ответ дал:
0
Рассмотрим ΔАВЕ - прямоугольный, ∠ВАЕ=∠ВЕА=45° по свойству острых углов прямоугольного треугольника. Значит, ΔАВЕ - равнобедренный, АВ=ВЕ=5. Тогда ЕС=17-5=12. Найдем ЕД из ΔСДЕ по теореме Пифагора:
ДЕ=√(СЕ²+СД²)=√(144+25)=√169=13 (ед.)
Ответ: 13.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад