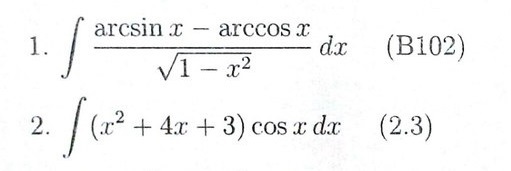Ответы
Ответ дал:
0
∫(arcsinx-arccosx)/√(1-x²)dx
∫arcsinx/√1-x²dx=∫arcsinxd(arcsinx)=arcsin²x/(2)
∫arccosx/√1-x²dx=∫arccosxd(-arccosx)=-arccos²x/(2)
исходный интеграл равен 0.5(arcsin²x+arccos²x)+C
-----------------------------
∫(x²+4x+3)cosxdx
∫x²cosxdx = интегрирование по частям -формула ∫fdg=fg-∫gdf
f=x² dg=cosxdx df=2xdx g=sinx
=x²sinx-2∫xsinxdx=
cнова по частям f=x dg=sinxdx df=dx g=-cosx
=x²sinx+2xcosx-2∫cosxdx=x²sinx+2xcosx-2sinx+c
4∫xcosxdx=4∫xd(sinx)=4xsinx-4∫sinxdx=4xsinx+4cosx+c
3∫cosxdx=3sinx+c
интеграл в целом равен x²sinx+2xcosx-2sinx+4xsinx+4cosx+3sinx
∫arcsinx/√1-x²dx=∫arcsinxd(arcsinx)=arcsin²x/(2)
∫arccosx/√1-x²dx=∫arccosxd(-arccosx)=-arccos²x/(2)
исходный интеграл равен 0.5(arcsin²x+arccos²x)+C
-----------------------------
∫(x²+4x+3)cosxdx
∫x²cosxdx = интегрирование по частям -формула ∫fdg=fg-∫gdf
f=x² dg=cosxdx df=2xdx g=sinx
=x²sinx-2∫xsinxdx=
cнова по частям f=x dg=sinxdx df=dx g=-cosx
=x²sinx+2xcosx-2∫cosxdx=x²sinx+2xcosx-2sinx+c
4∫xcosxdx=4∫xd(sinx)=4xsinx-4∫sinxdx=4xsinx+4cosx+c
3∫cosxdx=3sinx+c
интеграл в целом равен x²sinx+2xcosx-2sinx+4xsinx+4cosx+3sinx
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад